必要条件・十分条件と命題の証明方法(後編)
最終更新日:
この記事では「\(P\)ならば\(Q\)」型命題の証明方法と、「集合と命題」分野で頻出の必要条件・十分条件の判別問題を扱います。また、「\(P\)ならば\(Q\)」型命題の背理法による証明、対偶証明法との違い、数直線や座標平面を利用した必要条件・十分条件の判別方法について深掘りして詳しく解説していきます。
基礎から細かな注意点まで網羅したことでボリュームが多く、前後編に分かれていますが、最後まで読んでいただけると嬉しいです。 特に後編は例題を多めに設けたのでサクッと読みたい人は適宜スキップしてください。
目次
1. 命題の証明方法(前回の続き)
目次「\(P\)ならば\(Q\)」型命題の逆・裏・対偶
目次「\(P\)ならば\(Q\)」型命題の証明方法に入る前にこの形の命題で考える「逆・裏・対偶」という概念について説明します。
命題「\(P \Rightarrow Q\)」に対して,
- \(Q \Rightarrow P\)を逆
- \(\overline{P} \Rightarrow \overline{Q}\)を裏
- \(\overline{Q} \Rightarrow \overline{P}\)を対偶
といいます。
この関係を図にすると下のようになります。
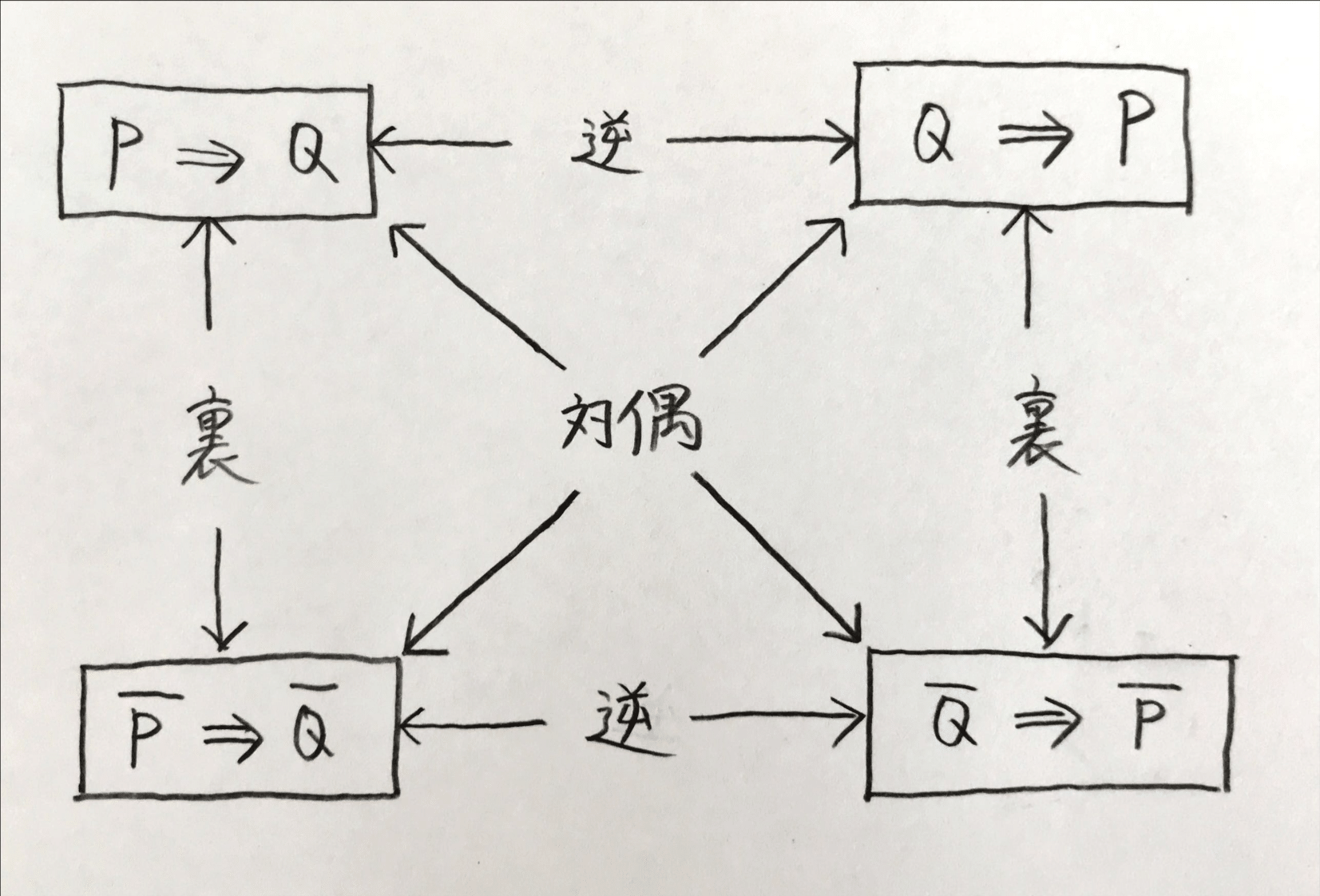
ベン図を書くと分かるようにもとの命題とその対偶の真偽は一致します。一方で、もとの命題と逆や裏は真偽が一致するとは限らないので注意しましょう。 また、逆の対偶は裏なので、逆と裏の真偽は一致します。
この問題は逆・裏・対偶が何かを正しく理解していれば、あとは条件の否定の知識を使って解けるので、復習にぴったりです。 それでは解いていきましょう。
ド・モルガンの法則を覚えていれば簡単です。
逆: 「\(a \leqq b\) または \(c \leqq d\) ならば \(a+c \leqq b+d\)」
裏: 「\(a+c > b+d\) ならば \(a > b\) かつ \(c > d\)」
対偶: 「\(a > b\) かつ \(c > d\) ならば \(a+c > b+d\)」
(2)はよく書く表記の意味を確認する問題です。\(\{\) と \(,\) は「かつ」・「または」に翻訳できるのですが、どちらの意味でしょうか。
今回の場合、正解は両方とも「かつ」です。ただし、\(,\) は状況によって「または」の意味で使われることもあり、実は意味が曖昧です。 もしも厳密に書きたいなら「かつ」・「または」や“and”, “or”を使ったほうがいいでしょう。
逆: 「\(x=1\) かつ \(y=1\) ならば \(x^2+y^2=2\) かつ \(y=x\)」
裏: 「\(x^2+y^2 \neq 2\) または \(y \neq x\) ならば \(x \neq 1\) または \(y \neq 1\)」
対偶: 「\(x \neq 1\) または \(y \neq 1\) ならば \(x^2+y^2 \neq 2\) または \(y \neq x\)」
「少なくとも1つ」の扱いがポイントです。前回の内容を覚えているでしょうか。
逆: 「\(a,\ b,\ c\)の少なくとも1つは0であるならば \(abc=0\)」
裏: 「\(abc \neq 0\) ならば \(a,\ b,\ c\)はすべて0でない」
対偶: 「\(a,\ b,\ c\)はすべて0でないならば \(abc \neq 0\)」
-
逆: 「\(a \leqq b\) または \(c \leqq d\) ならば \(a+c \leqq b+d\)」
裏: 「\(a+c > b+d\) ならば \(a > b\) かつ \(c > d\)」
対偶: 「\(a > b\) かつ \(c > d\) ならば \(a+c > b+d\)」
-
逆: 「\(x=1\) かつ \(y=1\) ならば \(x^2+y^2=2\) かつ \(y=x\)」
裏: 「\(x^2+y^2 \neq 2\) または \(y \neq x\) ならば \(x \neq 1\) または \(y \neq 1\)」
対偶: 「\(x \neq 1\) または \(y \neq 1\) ならば \(x^2+y^2 \neq 2\) または \(y \neq x\)」
-
逆: 「\(a,\ b,\ c\)の少なくとも1つは0であるならば \(abc=0\)」
裏: 「\(abc \neq 0\) ならば \(a,\ b,\ c\)はすべて0でない」
対偶: 「\(a,\ b,\ c\)はすべて0でないならば \(abc \neq 0\)」
さてこれらの命題は正しいでしょうか。これを確かめるために、次は「\(P\)ならば\(Q\)」型命題の証明方法を学習します。
「\(P\)ならば\(Q\)」型命題の証明方法
目次「\(P\)ならば\(Q\)」型命題とは「すべての\(x\)について『\(P(x)\)ならば\(Q(x)\)』」という形の命題だったので、これは前編で学んだ全称命題です。 前編のときと違うのは仮定\(P(x)\)を使うことができるので、これを使って\(Q(x)\)が真であることを示します。
前編の全称命題のときと同様に厳密な証明を紹介します。
全称命題「すべての\(x\)について\(P(x)\)」の証明では\(x\)を全体集合\(U\)の不特定の要素だと考えて命題\(P(x)\)が真であることを示せば、 すべての要素について成り立つことがいえるので証明できると説明しました。(前編参照、\(x\)を変数ではなく要素として考えていることに注意) この考え方を少しアレンジします。
前編の記事で「\(x\)が条件\(P(x)\)を満たさないときは条件\(Q(x)\)を満たしているか考える必要はない」と解説しました。 つまり、\(U\)の要素のうち条件\(P(x)\)を満たさないものは特に考えなくて大丈夫です。したがって、次のように変更します。
- 全体集合\(U\)の要素のうち「条件\(P(x)\)を満たす」不特定の要素\(a\)を条件\(Q(x)\)に代入して、命題\(Q(a)\)を考えます。
- 命題\(Q(a)\)が真であることを証明します。
前編のときと同様に形式的に\(a\)を\(x\)に置き換えれば 「\(P(x)\)を満たすことを使って\(Q(x)\)が真であることを証明する」という直感通りの説明とつじつまが合います。
偽であることを示す場合は全称命題なので反例が存在することを示します。反例は「条件\(P(x)\)を満たし、かつ、条件\(Q(x)\)を満たさないもの」です。 なぜこうなるのかは「\(P\)ならば\(Q\)」型命題の否定を考える必要があるのですが、実はこのときに前回の記事「必要条件・十分条件と命題の証明方法(前編)」 の補足「Q. 「すべての」が付いて命題になるなら「\(P(x)\)ならば\(Q(x)\)」は条件ではないですか?」で説明した内容が役立ちます。
条件「\(P(x)\)ならば\(Q(x)\)」は条件「『\(P(x)\)でない』または『\(Q(x)\)』」と同値です。 このことから考えると、反例が「条件\(P(x)\)を満たし、かつ、条件\(Q(x)\)を満たさないもの」であることが理解できると思います。
続いて、背理法(で真であることを示す場合)の説明です。 「偽のときの方法で進めて矛盾を示す」ので、「条件\(P(x)\)を満たし、かつ、条件\(Q(x)\)を満たさないものが存在する」と仮定して矛盾を示します。
筆者が背理法を学んだときは「無理数である」ことの証明例ばかり出てきて「\(P\)ならば\(Q\)」型命題の例を見かけなかったので理解があやふやでした。 「\(P\)ならば\(Q\)」型命題は厳密に考えると意外と複雑で背理法になるとその複雑さが表れてくるので注意してください。
最後に「\(P\)ならば\(Q\)」型命題特有の対偶証明法について解説します。先程、もとの命題とその対偶の真偽は一致することを紹介しました。 これを利用して、命題\(P(x) \Rightarrow Q(x)\)が真であることを証明するのに命題\(\overline{Q} \Rightarrow \overline{P}\)が真であることを示す方法を対偶証明法といいます。
もとの命題よりその対偶の方が証明しやすいときに役立ちます。これで説明は終わりです。例題を解いて証明方法をマスターしましょう。
次の各命題の真偽を答えてください。さらに、真である場合には証明し、偽である場合には反例を挙げてください。ただし、各文字は実数とします。
- \(x^2-8x+15=0\) ならば \(x=3\) または \(x=5\) または \(x=7\)
- \(\sqrt{x^2}=y\) ならば \(x=y\)
- \(a+c \leqq b+d\) ならば \(a \leqq b\) または \(c \leqq d\)
- \(\begin{cases} x^2+y^2=2\\ y=x \end{cases}\) ならば \(x=1,\) \(y=1\)
※各解説・解答からこの例題に戻れます
仮定が2次方程式なので解くことができます。\(x^2-8x+15=0\)を解くと、\(x=3\) または \(x=5\) なので、 \(x\)がこれを満たすとき当然 \(x=3\) または \(x=5\) または \(x=7\)を満たします。よって、命題は真です。 結論に\(x=7\)という余分なものが付いていますが「または」の意味を考えるとわかるように気にしなくて大丈夫です。
\(\sqrt{x^2}\)の扱いを覚えているでしょうか。\(\sqrt{x^2} = |x|\)です。つまりこの命題は「\(|x|= y\) ならば \(x=y\)」 と言い換えることができます。 これは\(x\)が負のとき成り立ちません。なので具体例を1つ挙げて反例として示します。
命題は偽、反例は\(x=-1,\) \(y=1\)
\(\sqrt{x^2} = y \Leftrightarrow |x| = y\)です。絶対値を付けるのを忘れないようにしましょう。
(3), (4)は例題1で出てきた命題です。今回は証明してみましょう。 ここで、対偶証明法を使う一つの目安として結論に「または」や「少なくとも」が含まれるときは対偶が証明しやすいことが多いです。 なぜかというと、結論に「または」が含まれるときに対偶を考えると、仮定に「かつ」が来るからです。 というわけで(3)は対偶を利用して示します。
対偶: 「\(a > b\) かつ \(c > d\) ならば \(a+c > b+d\)」を考えるとこれは真です。したがって、もとの命題も真になります。
一見正しそうですが、反例\(x=-1,\) \(y=-1\)が存在するので、命題は偽です。
ところで、この反例はどのように見つけるのでしょうか。このとき有効なのが数式を数直線や座標平面を使って捉える方法です。 この考え方については例題4 必要条件・十分条件で詳しく解説します。
- 真: 仮定より\(x=3\) または \(x=5\). このとき \(x=3\) または \(x=5\) または \(x=7\) を満たすので真
- 偽: 反例は\(x=-1,\) \(y=1\)
- 真: 対偶「\(a > b\) かつ \(c > d\) ならば \(a+c > b+d\)」が真なので、もとの命題も真
- 偽: 反例は\(x=-1,\) \(y=-1\)
続いて難易度が高めの例題も見てみます。 整数分野の知識が必要となるのでわからないかもしれませんが、 「\(P\)ならば\(Q\)」型命題の証明の解答の流れは参考になると思います。
結論に「無理数である」と見えるので、前編の「\(\sqrt{2}\)が無理数であること」の証明を思い出して、背理法を考えます。 つまり、「『\(\sqrt{m}\)が整数でない』かつ『\(\sqrt{m}\)は有理数』」であるような自然数\(m\)が存在すると仮定して矛盾を示します。
\(\sqrt{2}\)のときと同じく、有理数であることを数式で表すときは\(\sqrt{m}=\dfrac{p}{q}\) \(\left(\dfrac{p}{q} \text{は既約分数}\right)\)とおきます。 さらに、\(\sqrt{m}\)が整数でないので\(q \neq 1\)です。
このとき両辺を2乗すると\(m=\left(\dfrac{p}{q}\right)^2\)となり、\(\dfrac{p}{q}\)は既約分数で\(q \neq 1\)なので右辺は整数ではありませんが、 これは\(m\)が自然数であることと矛盾します。
以上から背理法の仮定が間違っていることが示せたので、命題が真であることが証明できました。
無理数であることの証明なのでまた同じように考えるのかなと思いますが、問題をよく見てください。 複雑な問題では前の問題の結果を利用することがあります。 今回の場合(1)より\(m\)が自然数のときは、\(\sqrt{m}\)が無理数であることを示すには\(\sqrt{m}\)が整数でないことを示せば十分です。 また、前提条件を確認すると\(n\)が3以上の整数より、\(n^2+5\)は自然数なので(1)の結果が使える状況になっています。
整数でないことの証明ですが、今回も背理法を使いましょう。 整数であると仮定して文字でおいて議論を進め、矛盾を示すほうが直接示そうとするより扱いやすいからです。 背理法をいつ使うべきかについては次回の記事「背理法の使い時まとめと複数の文字を含む条件」で考察します。
\(\sqrt{n^2+5}\)が整数であると仮定して、\(\sqrt{n^2+5}=k\)とおきます。(\(k\)は自然数)
両辺を2乗して、
\begin{align} &n^2+5=k^2\\[0.7em]&k^2-n^2=5\\[0.7em]&(k+n)(k-n)=5 \end{align}
因数分解することにより、掛けて5になる組を探せばよいことがわかります。 さらに条件を上手く活用すると\(k,n\)は自然数なので、\(k+n > 0,\) \(k+n > k-n\) です。
よって、\(k+n=5,\) \(k-n=1\)のパターンに限定されます。 これを解くと、\(k=3,\) \(n=2\)となりますが、これは\(n\)が3以上の整数であることに矛盾します。
したがって、\(\sqrt{n^2+5}\)は整数ではないことが示されました。 そして、\(n^2+5\)は自然数なので(1)より、\(\sqrt{n^2+5}\)は無理数となります。
-
背理法で示す
\(\sqrt{m}\)が整数でないかつ\(\sqrt{m}\)は有理数を満たす自然数\(m\)が存在すると仮定する
自然数\(p,q\)を用いて\(\sqrt{m}=\dfrac{p}{q}\) \(\left(\dfrac{p}{q} \text{は既約分数}\right)\)とおくと, \(\sqrt{m}\)が整数でないことから\(q \neq 1\)
\(\sqrt{m}=\dfrac{p}{q}\)の両辺を2乗すると\(m=\left(\dfrac{p}{q}\right)^2\)
ここで\(\dfrac{p}{q}\)は既約分数かつ\(q \neq 1\)から右辺は整数でないが、これは\(m\)が自然数であることに矛盾する
したがって, \(\sqrt{m}\)が整数でなければ、\(\sqrt{m}\)は無理数である
-
\(n\)が3以上の整数だから\(n^2+5\)は自然数である
このとき(1)より, \(\sqrt{n^2+5}\)が整数でなければ、\(\sqrt{n^2+5}\)は無理数である
\(\sqrt{n^2+5}\)が整数でないことを背理法で示す
\(\sqrt{n^2+5}\)が整数であると仮定して\(\sqrt{n^2+5}=k\)(\(k\)は自然数)とおくと
\begin{align} &n^2+5=k^2\\[0.7em]&k^2-n^2=5\\[0.7em]&(k+n)(k-n)=5 \end{align}
\(k,n\)は自然数なので、\(k+n > 0,\) \(k+n > k-n\) より \(k+n=5,\) \(k-n=1\)
よって, \(k=3,\) \(n=2\)となるが、これは\(n\)が3以上の整数であることに矛盾
したがって、\(\sqrt{n^2+5}\)は整数ではないので無理数である
ところで、「\(P\)ならば\(Q\)」型命題の間接証明法には背理法と対偶証明法がありますが、 この2つはどのように違うのでしょうか。補足としてまとめたので気になる人はご覧ください。
A. 結論を先に言うと、「\(P\)ならば\(Q\)」型命題の背理法と対偶証明法は実は本質的には同じです。しかし、使い勝手は違うので問題によってやりやすい方を選びましょう。
まず、なぜ本質的に同じなのか説明します。対偶証明法では\(\overline{Q} \Rightarrow \overline{P}\)が成り立つことを示しますが、 結論が\(\overline{P}\)になるのは言い換えると\(P\)にはならないことを意味します。つまり、\(\overline{Q}\)かつ\(P\)を満たすものは存在しないことを示しています。 これは背理法のときの考え方と同じです。
このように本質は同じですが、実際に使うときの感覚は違います。使い分けを考えると、対偶証明法が簡単そうならそちらを使い、困ったなら背理法を使うのがおすすめです。 次はなぜこのような使い分けをするのかについて解説します。
対偶証明法はスタートとゴールが明確です。スタートは\(\overline{Q}\)、ゴールは\(P\)ですね。なので、解くときに証明の全体の流れがつかみやすいです。 一方、背理法はゴールが曖昧です。「矛盾を示すこと」がゴールですが、どこでどうやって矛盾を示すのかは自由です。これが背理法が難しく感じる原因の一つです。 しかし、その分スタートの材料が多くなっていて、\(\overline{Q}\)と\(P\)の両方を使うことができます。
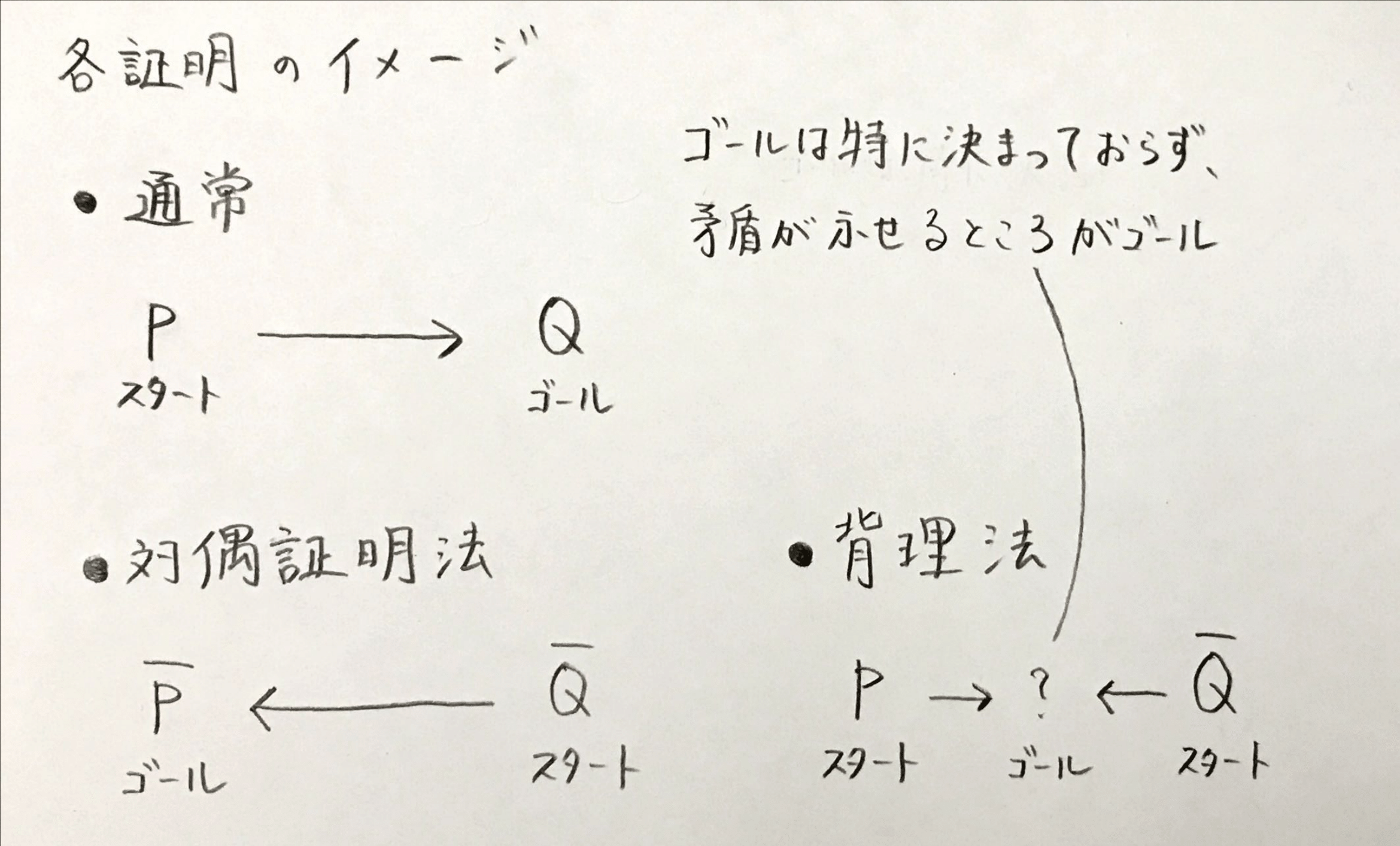
つまり、背理法はスタートの材料が多く、ポテンシャルは高いタイプなのですが、その分扱いが難しいわけです。 なので、とりあえず対偶証明法を使ってみて、上手くいかないなら背理法を使うのがいいと思います。
さて、これで「\(P\)ならば\(Q\)」型命題の証明方法も学習したのでいよいよ頻出である必要条件・十分条件を判別する問題に進みましょう。
2. 必要条件・十分条件の判別
目次確認ですが、「\(P\)ならば\(Q\)」型命題の真偽と必要条件・十分条件の関係は下の表のようになります。
| 「\(P \Rightarrow Q\)」と「\(Q \Rightarrow P\)」の真偽 | \(P\)は\(Q\)の… |
|---|---|
| 「\(P \Rightarrow Q\)が偽」かつ「\(Q \Rightarrow P\)が真」 | 必要条件であるが, 十分条件ではない |
| 「\(P \Rightarrow Q\)が真」かつ「\(Q \Rightarrow P\)が偽」 | 十分条件であるが, 必要条件ではない |
| 「\(P \Rightarrow Q\)が真」かつ「\(Q \Rightarrow P\)が真」 | 必要十分条件である |
| 「\(P \Rightarrow Q\)が偽」かつ「\(Q \Rightarrow P\)が偽」 | 必要条件でも十分条件でもない |
必要条件・十分条件を考えるときは冷静にこの判断方法を思い出しましょう。それでは例題です。
次の空欄に当てはまるものを下の選択肢(a)~(d)から1つずつ選んでください。
- 「\(|x| \leqq 1\)」は「\(x \leqq 1\)」であるための空欄である
- 「『\(-2 < x \leqq 5\)』または『\(-5 < x \leqq 2\)』」は 「『\(-2 < x \leqq 5\)』かつ『\(-5 < x \leqq 2\)』」であるための空欄である
- 「\(x^2+y^2 \leqq 2\)」は「『\(|x| \leqq 1\)』かつ『\(|y| \leqq 1\)』」であるための空欄である
- 「\(x^2+y^2 \leqq 2\)」は「\(|x|+|y| \leqq 2\)」であるための空欄である
- 「\(|x+y| \leqq 1\)」は「『\(|x| \leqq 1\)』かつ『\(|y| \leqq 1\)』」であるための空欄である
※各解説・解答からこの例題に戻れます
「\(P \Rightarrow Q\)」と「\(Q \Rightarrow P\)」の真偽を調べるのですが、ここで実はいい方法があります。 今回のように条件が式で表されている場合は以下の考え方が使えないか検討しましょう。
1変数は数直線、2変数は座標平面の利用を考える
この方法は条件を直感的に捉えることができ、必要条件・十分条件の判別も視覚的に行うことができるのでとても有効です。 どのように数直線や座標平面を使うのか実際に例題を解きながら見ていきます。
「\(|x| \leqq 1\)」を満たすのは絶対値の定義より、数直線上で原点からの距離が1以下の点になります。つまり、\(-1 \leqq x \leqq 1\)と同値です。 絶対値の処理については「1次不等式・絶対値と場合分け」で解説していますが、このような図形的解釈のイメージも大切です。
数直線を使って以上以下・より大きい・未満を表現するときは下の図のように書くとわかりやすいです。
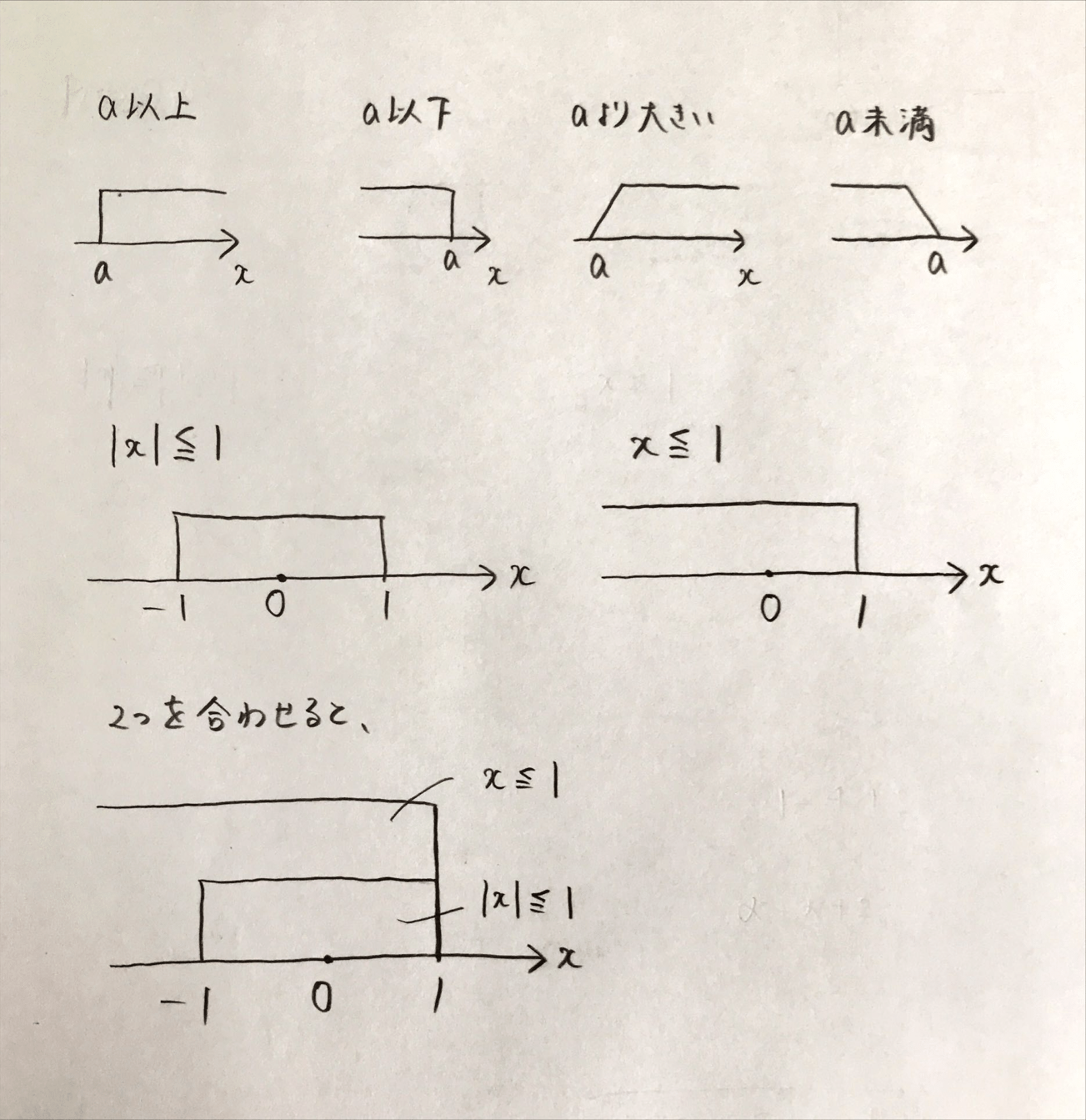
この数直線の図をベン図のように見れば必要条件・十分条件の判別が直感的にできます。答えは(b)です。
このように、数直線や座標平面を利用し視覚的に捉えることで数式のままで解くよりも直感的に、そして速く解けるので利用できないか意識するようにしましょう。 これは必要条件・十分条件の問題以外でも出てくる考え方なので覚えておきましょう。
実は今回の問題は全て数直線や座標平面が利用できる形になっています。というわけで、それぞれの数式がどのように表されるのか見ていきましょう。
(2)は(1)でやった数直線の利用に「かつ」・「または」を組み合わせる問題です。実際に描いてみると下の図のようになります。
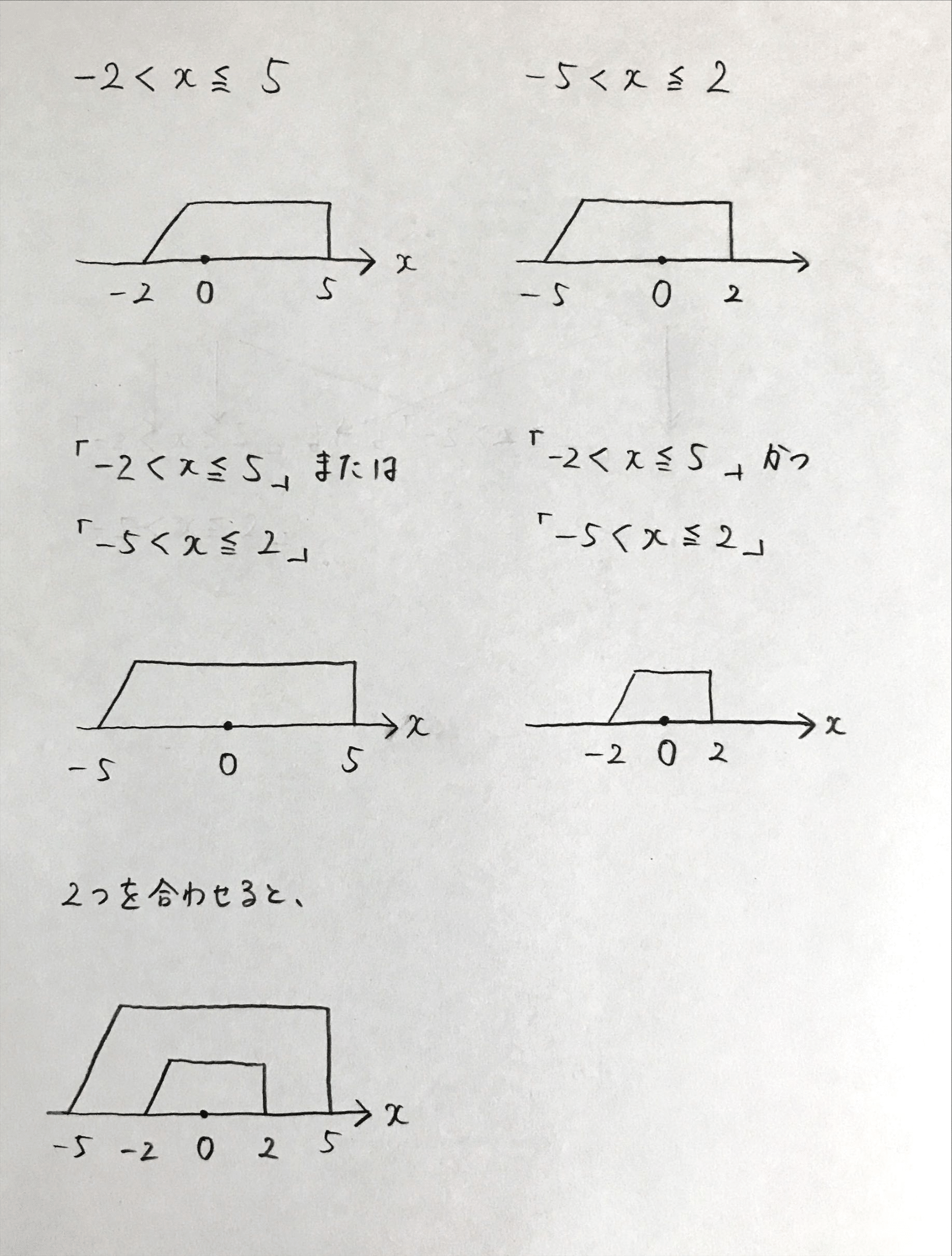
したがって答えは(a)です。
(3), (4), (5)は2変数なので座標平面で考えます。「座標平面」という言葉が聞きなれない人もいるかもしれませんが、グラフを書く時に考える、\(x\)軸と\(y\)軸が引かれた平面のことです。
座標平面で数式がどのように表されるのか見てみましょう。まず、\(x^2+y^2\)は原点からの距離の2乗を表します。これは三平方の定理が根拠となります。 この分野に限らずよく出てくる形なので記憶に留めておくといいでしょう。 今回は原点からの距離の2乗が2以下、つまり原点からの距離が\(\sqrt{2}\)以下となります。この条件を満たす点を集めて図示するとどうなるか考えてみましょう。
続いて\(|x| \leqq 1\)は\(x\)軸方向、つまり横方向の距離が原点から1以下となります。\(|y| \leqq 1\)も同様に考えます。 どんな領域になるか想像できたでしょうか。正解は下の図のようになります。
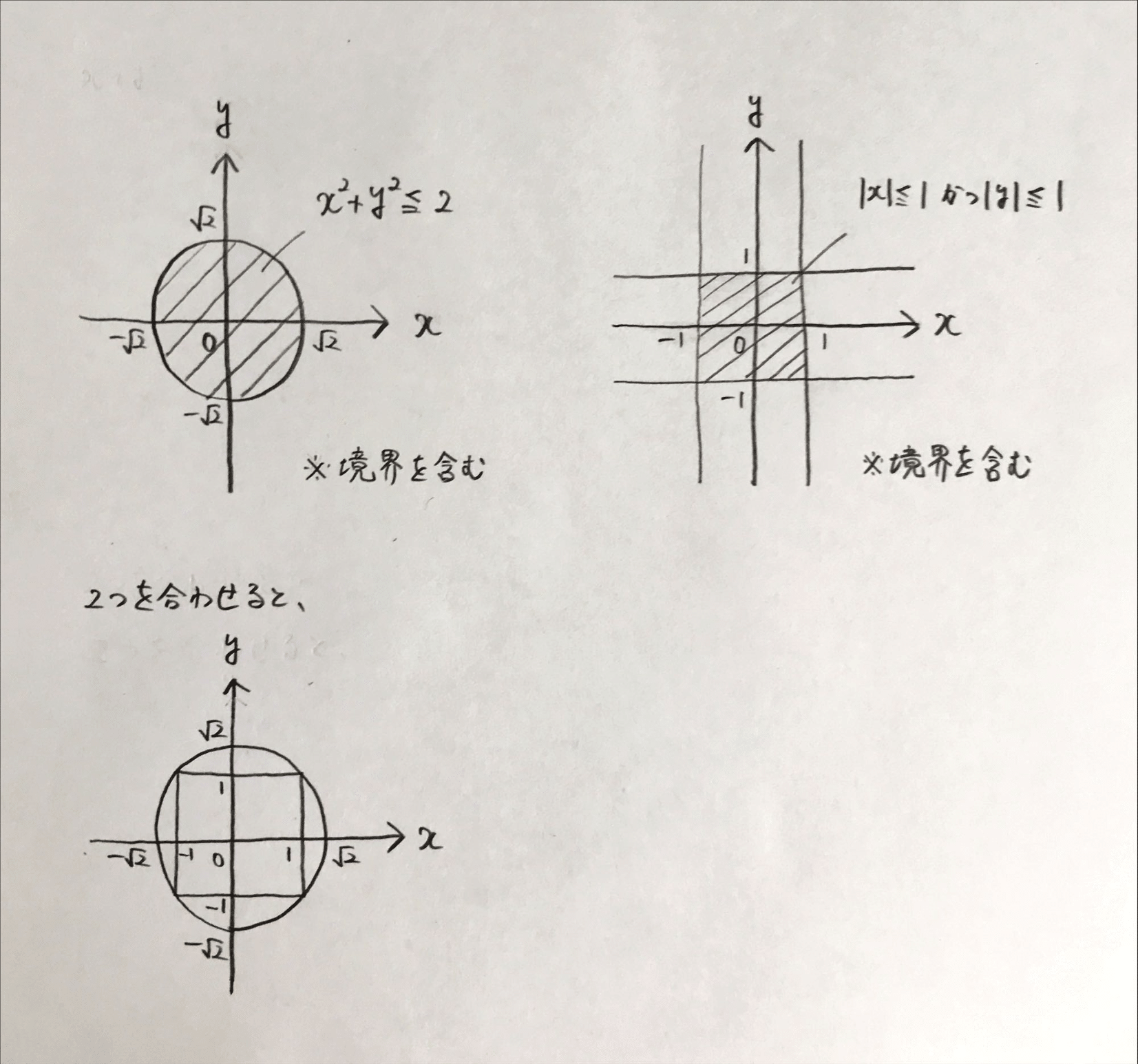
よって答えは(a)になります。 なお、図を描くにあたって数直線のときは端点を含む・含まないを上手くかき分けることができましたが、座標平面では難しいので日本語で明記します。
\(x^2+y^2\)は(3)で登場しました。今回のポイントは\(|x|+|y|\)です。(3)から類推すると(横方向の距離)\({} + {}\)(縦方向の距離)ですね。それが2以下なので原点からあまり遠くには行けなさそうです。 ここまでのヒントでどのような形になるかイメージできたでしょうか。
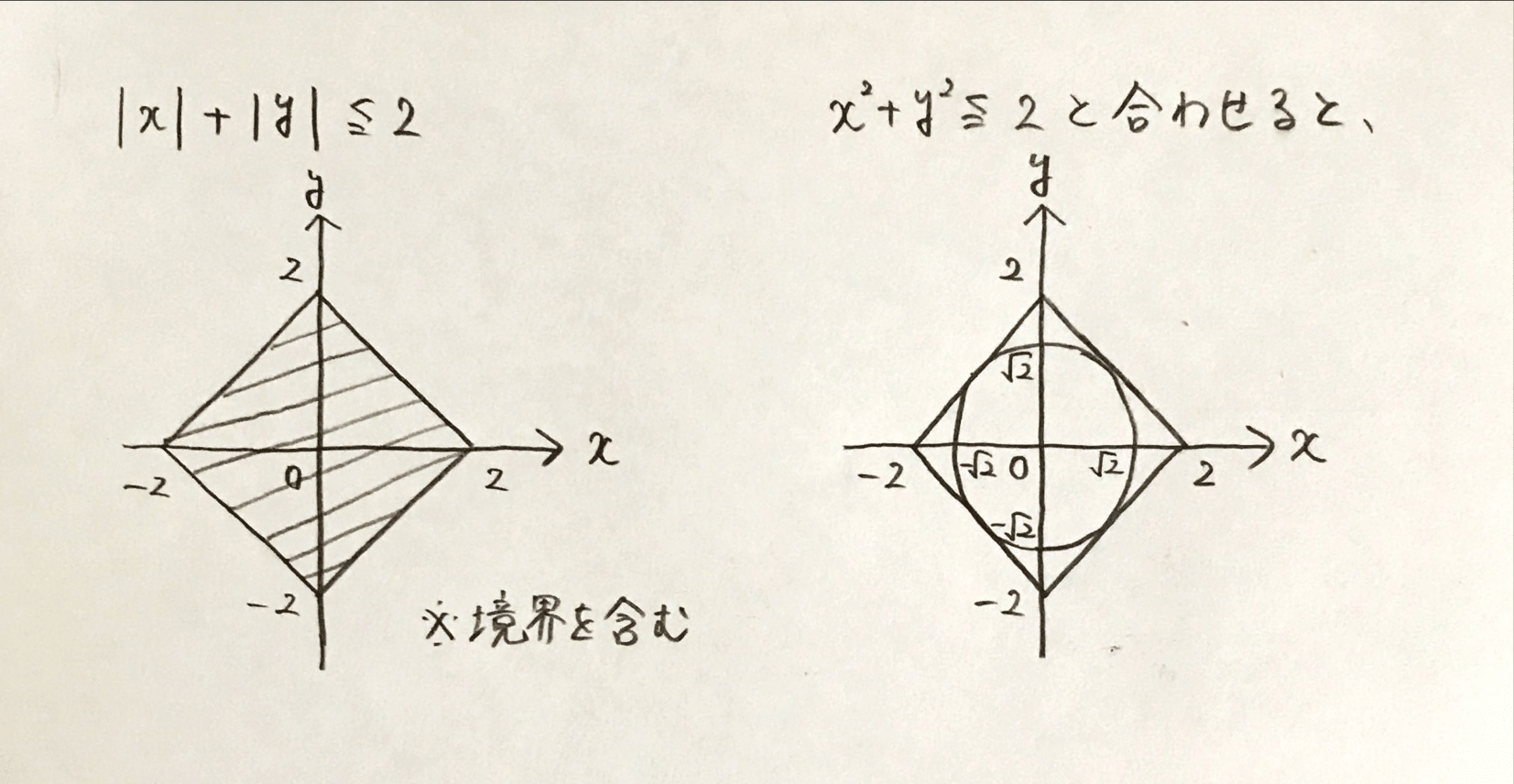
正解はこんな感じでした。図が分かれば答えはすぐわかります。(4)は(b)が正解です。
(5)は\(|x+y|\)が初見です。絶対値の処理と数Ⅱの図形と方程式分野の知識がないと少し難しいかもしれません。なので今回は結果だけ覚えておくでもいいです。 \(|x+y| \leqq 1 \Leftrightarrow -1 \leqq x+y \leqq 1 \Leftrightarrow {}\)「\(y \geqq -x-1\)」かつ「\(y \leqq -x+1\)」より下の図のような帯状の領域になります。
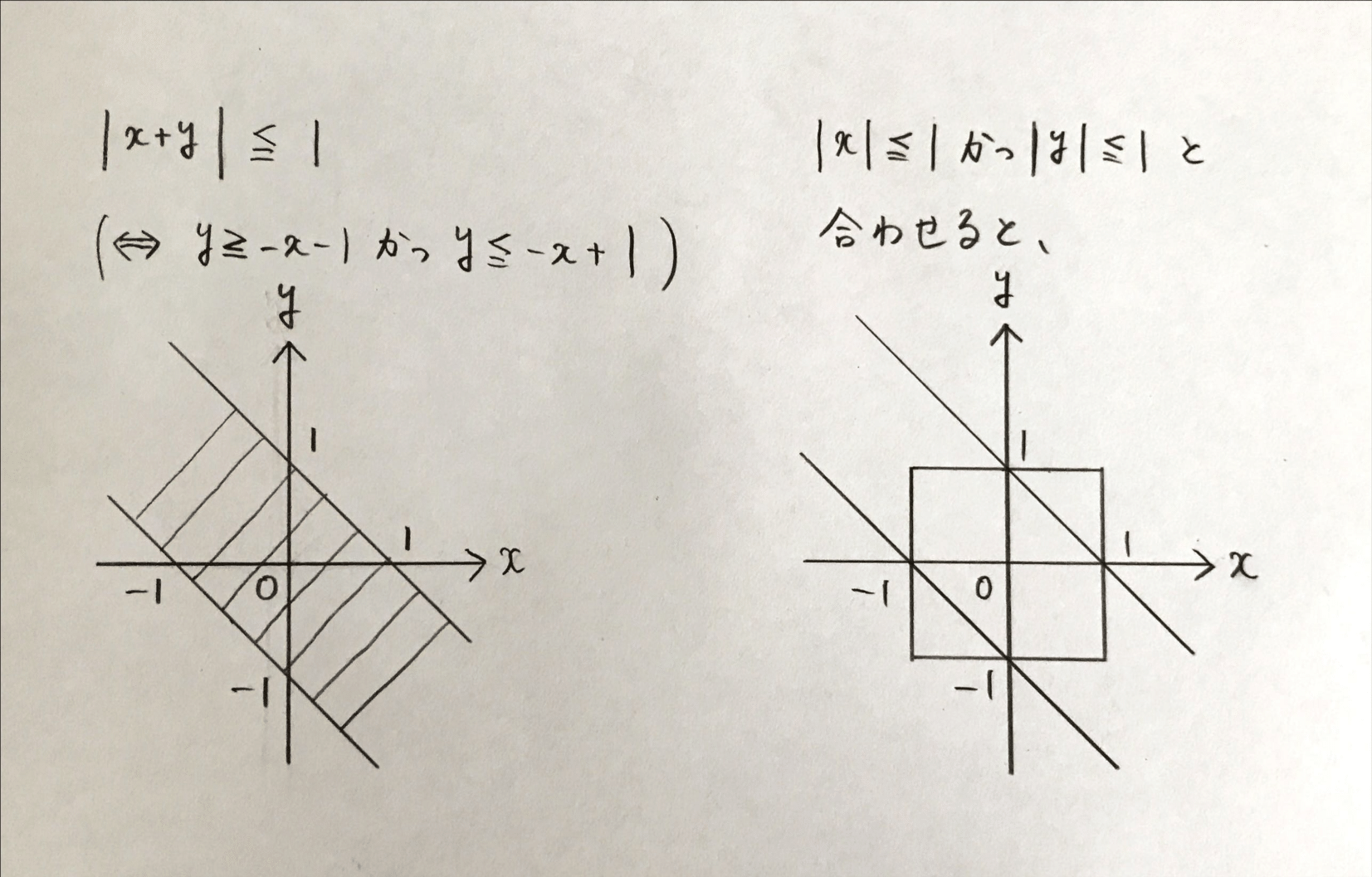
図より(d)が答えとなります。数直線・座標平面の威力が伝わったでしょうか。先程の例題2の(4)もこの方法を使うと反例がすぐ見つかります。
- (b)
- (a)
- (a)
- (b)
- (d)
必要条件・十分条件の意味とその判別方法は理解できたでしょうか。最後に応用として捻りの効いた問題を解いてこの記事を終わりにしたいと思います。
実数\(x\)に対して次の3つの条件\(P(x),\) \(Q(x),\) \(R(x)\)を考えます。(\(a\)には何かしらの数字が入ると思ってください。)
- \(a\)を整数とします。\(a\)の値を決めると\(P(x),\) \(Q(x),\) \(R(x)\)は\(x\)についての条件となりますが、 そのときに\(Q(x)\)が\(P(x)\)であるための十分条件となり、かつ、\(Q(x)\)が\(R(x)\)であるための必要条件となるような整数\(a\)の値をすべて求めてください。
(2次不等式が未学習の方へヒント \(x^2+ax+b < 0\)の解は\(x^2+ax+b=0\)の解を\(\alpha ,\ \beta\) \((\alpha < \beta)\)とすると、\(\alpha < x < \beta\)となります)
※各解説・解答からこの例題に戻れます
先程までは必要条件・十分条件を判断する問題でしたが、今回は必要条件・十分条件となるような整数\(a\)の値を求める問題です。 難易度は高いですが今までの知識を利用して一つずつ解いていきましょう。
1変数についての条件なので、それぞれの条件がどのように数直線で表されるのか考えていきましょう。
まず条件\(P(x)\)について\(|x-6|\)の意味を\(|x|\)から類推できるでしょうか。これは点6からの距離を表します。 \(|x|=|x-0|\)と考えると対応関係が分かりやすいと思います。なので条件\(P(x)\)は点6からの距離が4以下という条件です。
条件\(R(x)\)はそのままですが、問題は条件\(Q(x)\)です。初手が見えるとわかりやすいと思います。\((a^2+a-6)\)と\(-(2a+1)\)の関係に注目してみましょう。
正解は因数分解です。この式は因数分解することでより簡単な式にすることができます。ヒントを見ると\((\text{左辺})=0\)の2次方程式を考えればいいようです。 \(x^2-(2a+1)x+(a^2+a-6)= {} \)\(\{x-(a-2)\}\{x-(a+3)\}\) より、\(x=a-2\) または \(a+3\)です。 ここで\(a\)の値によらず、\(a-2 < a+3\)なので、ヒントから条件\(Q(x)\)は\(a-2 < x < a+3\)と言い換えることができます(同値変形)。 これで3つの条件が図示できる形になったので\(a\)に具体的な値を入れて調べてみましょう。
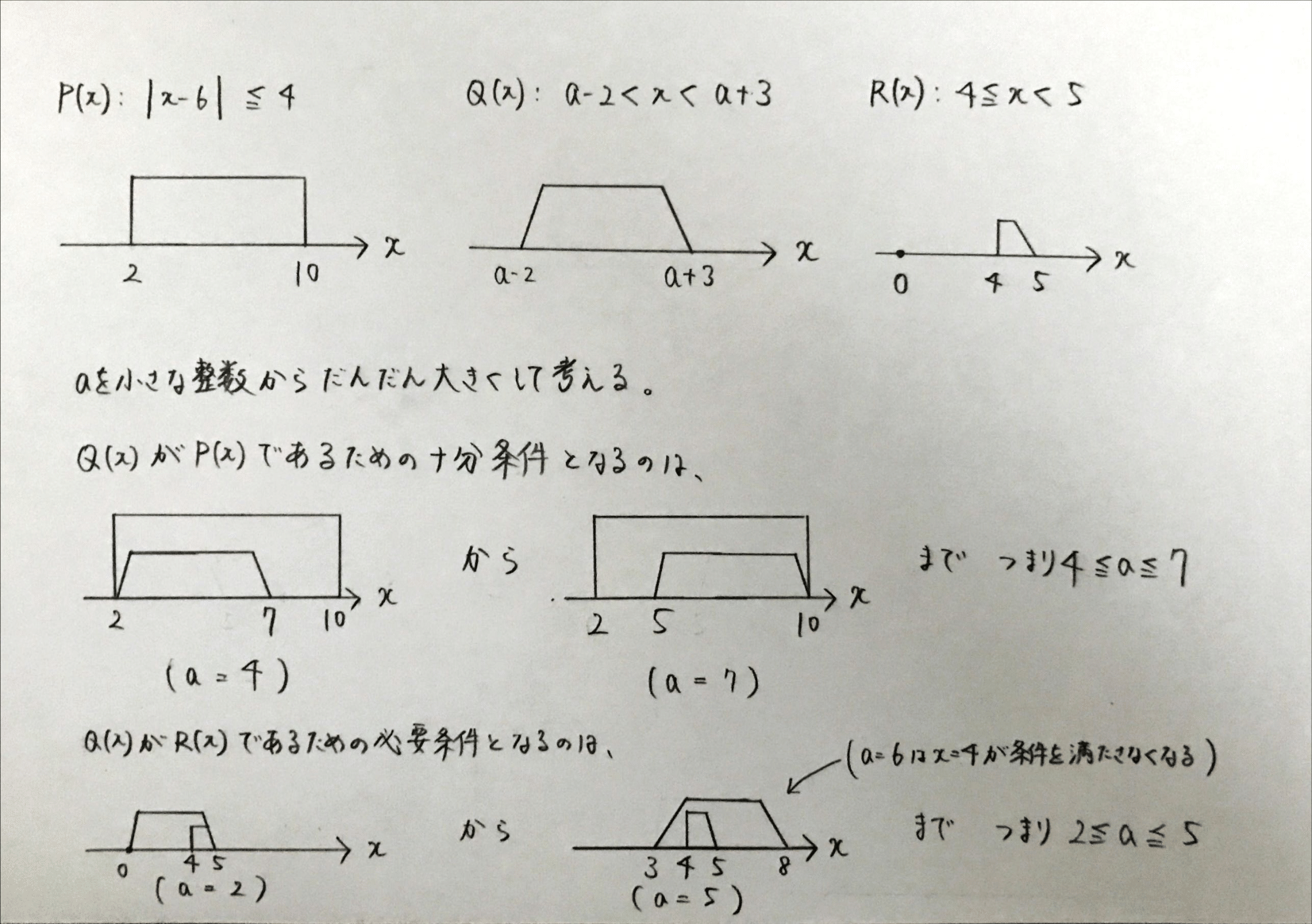
したがって答えは\(a=4, 5\)となります。今回の問題では領域の端にも注意する必要がありました。
- \(a=4, 5\)
3. まとめと次回予告
目次まとめ
目次今回の内容をまとめると、
- 「\(P\)ならば\(Q\)」型命題には逆・裏・対偶があり、もとの命題とその対偶の真偽は一致する。
- 「\(P\)ならば\(Q\)」型命題の反例は条件\(P(x)\)を満たし、かつ、条件\(Q(x)\)を満たさないもの、背理法ではこれが存在すると仮定する。
- 「\(P\)ならば\(Q\)」型命題の証明で対偶証明法と背理法は本質的には同じ。 しかし使い勝手は違い、背理法のほうがポテンシャルは高いが扱いが難しいのでまずは対偶証明法を使うのがおすすめ。
- 2つの命題「\(P \Rightarrow Q\)」と「\(Q \Rightarrow P\)」の真偽によって必要条件・十分条件が判別できる。
- 1変数の条件は数直線、2変数の条件は座標平面で考えることを試みる。
次回予告
目次背理法は慣れないと使うのが難しいです。そこで次回は背理法をよく使う場面をまとめて紹介します。 また、今回の例題5について実は条件\(Q(x)\)がそのままだと\(a\)と\(x\)の2文字についての条件になっているので難易度が上がっています。 このように複数の文字を含む条件は今後も出てくるので慣れておかなければなりません。そこで次回は複数の文字を含む条件の解説もしていきます。 「すべての」・「ある」が再登場するのでお楽しみに。