必要条件・十分条件と命題の証明方法(前編)
最終更新日:
今回は「集合と命題」分野でよく出題される必要条件・十分条件の紹介といろいろな形の命題の証明方法を解説します。分かりにくいところは直感的な説明を加えていきます。基礎から細かな注意点まで網羅したことでボリュームが多く、前後半に分かれていますが、最後まで読んでいただけると嬉しいです。
目次
1. 命題「\(P\)ならば\(Q\)」
目次数学でよく出てくる命題の形として「\(P\)ならば\(Q\)」という形式があります。これはどういう意味なのでしょうか。
必要条件・十分条件と集合の包含関係
目次まず、2つの条件を用意します。ここでは\(x\)についての条件として\(P(x),\) \(Q(x)\)で表します。 これらの条件を使って「すべての\(x\)について『\(P(x)\)ならば\(Q(x)\)』」を考えます。 前回の記事「集合と命題を学ぶ理由と集合・命題・条件の基本」で解説したように、これは条件に「すべての」が付いているので命題になります。 そして、この命題を\(P(x) \Rightarrow Q(x)\)とも書きます。
このとき条件\(P(x)\)を仮定、条件\(Q(x)\)を結論といいます。 この命題は\(x\)が条件\(P(x)\)を満たすとき必ず条件\(Q(x)\)も満たす場合は真となり、それ以外は偽となります。 \(x\)が条件\(P(x)\)を満たさないときは条件\(Q(x)\)を満たしているか考える必要はないです。
さらにこの命題が真であるとき2つの条件にはそれぞれ特別な名前が付きます。 条件\(Q(x)\)は条件\(P(x)\)であるための必要条件であるといい、 反対に条件\(P(x)\)は条件\(Q(x)\)であるための十分条件であるといいます。
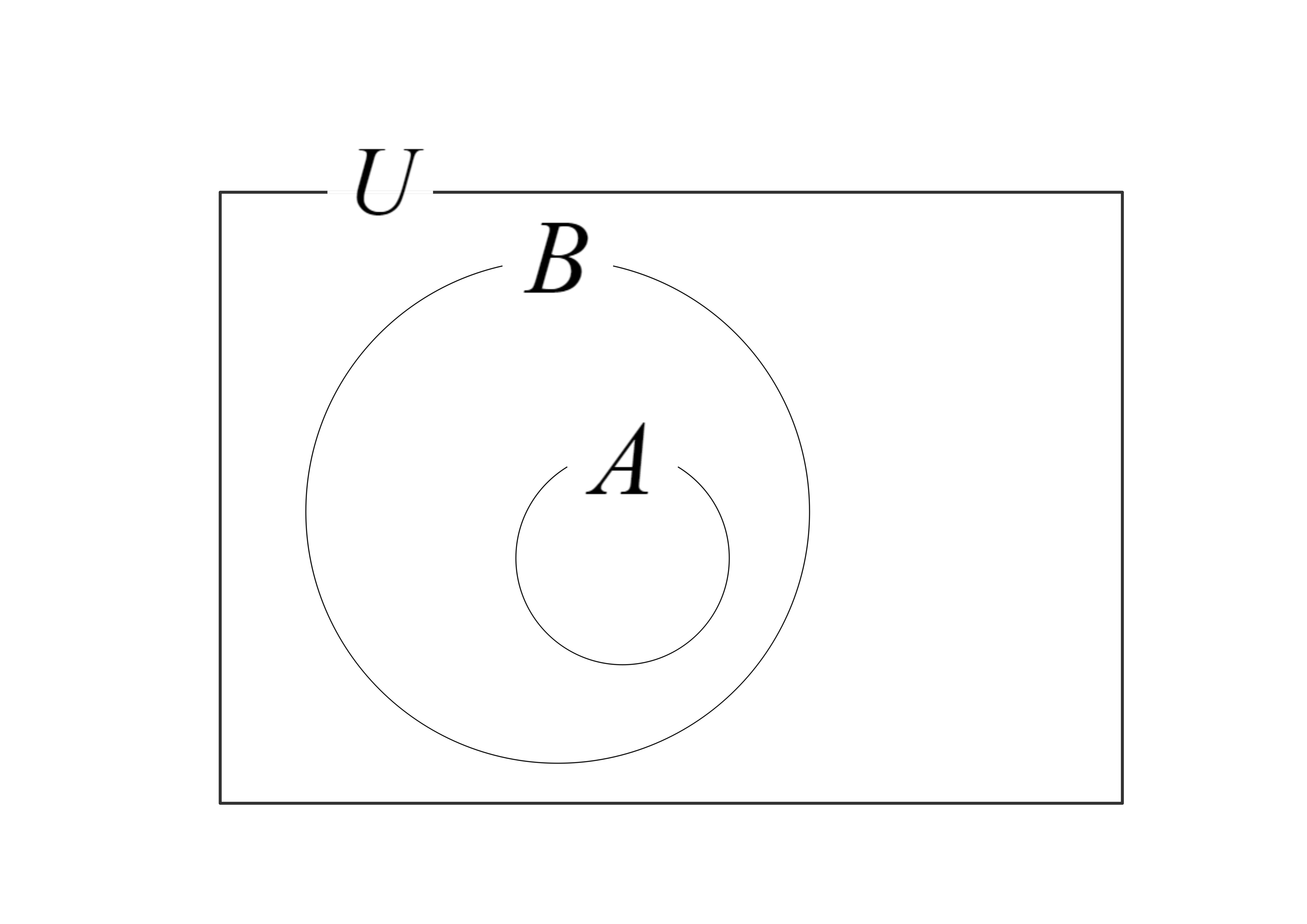
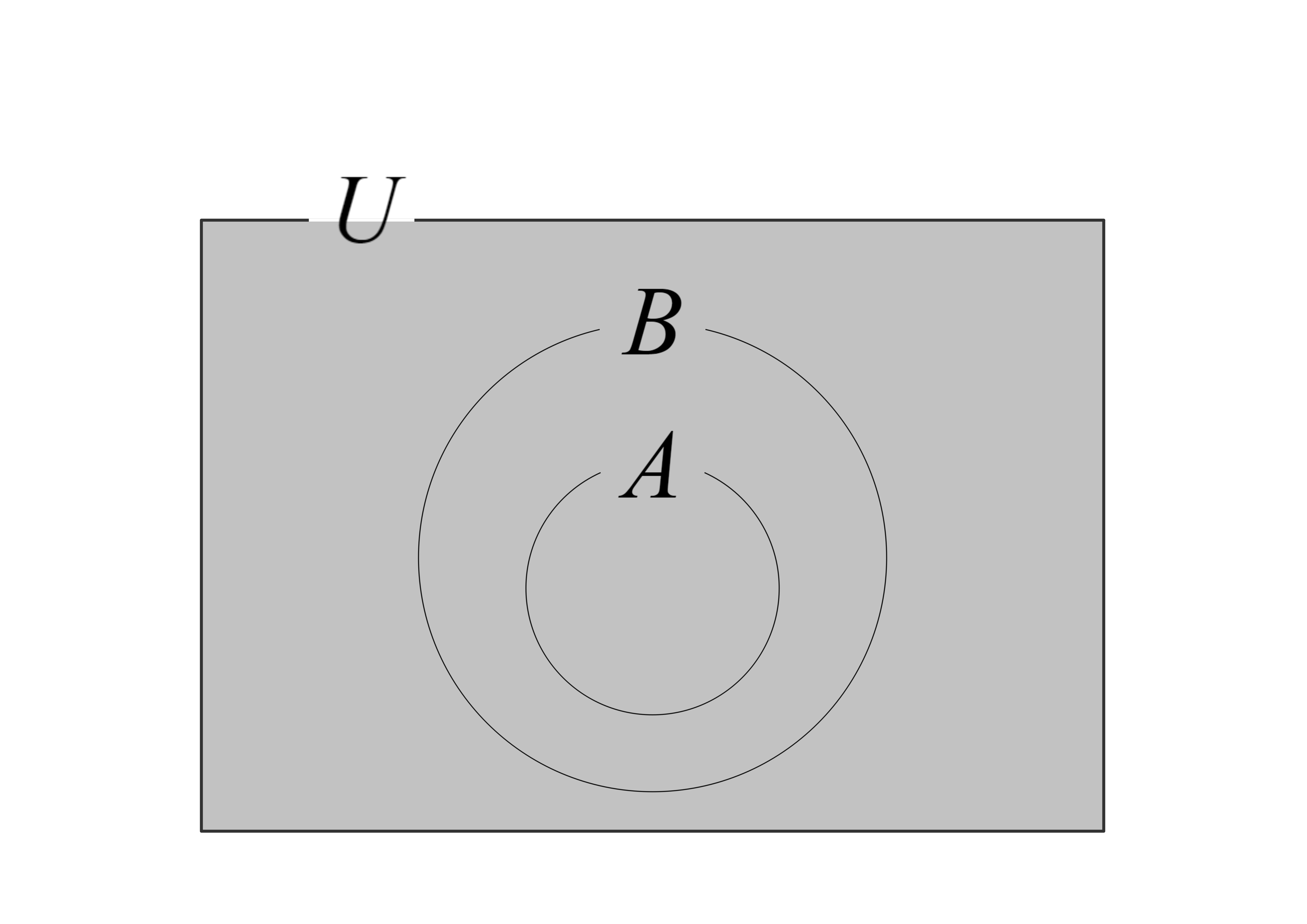
集合との関係も見てみましょう。条件\(P(x),\) \(Q(x)\)の真理集合をそれぞれ\(A,\) \(B\)とします。 \(P(x) \Rightarrow Q(x)\)が真のとき「すべての\(x\)について『\(x \in A\)ならば\(x \in B\)』」であるといえます。 このとき集合\(A\)は集合\(B\)の部分集合であるといい、\(A \subset B\)(\(B \supset A\)でも同じ)で表します。 日本語では「\(A\)は\(B\)に含まれる」・「\(B\)は\(A\)を含む」といいます。この状況をベン図で表すと下のようになります。
身近な場面で考える必要条件・十分条件
目次この必要条件・十分条件を問う問題が頻出なのですが、初めはイメージがつかみにくいので日常の場面で考えてみましょう。
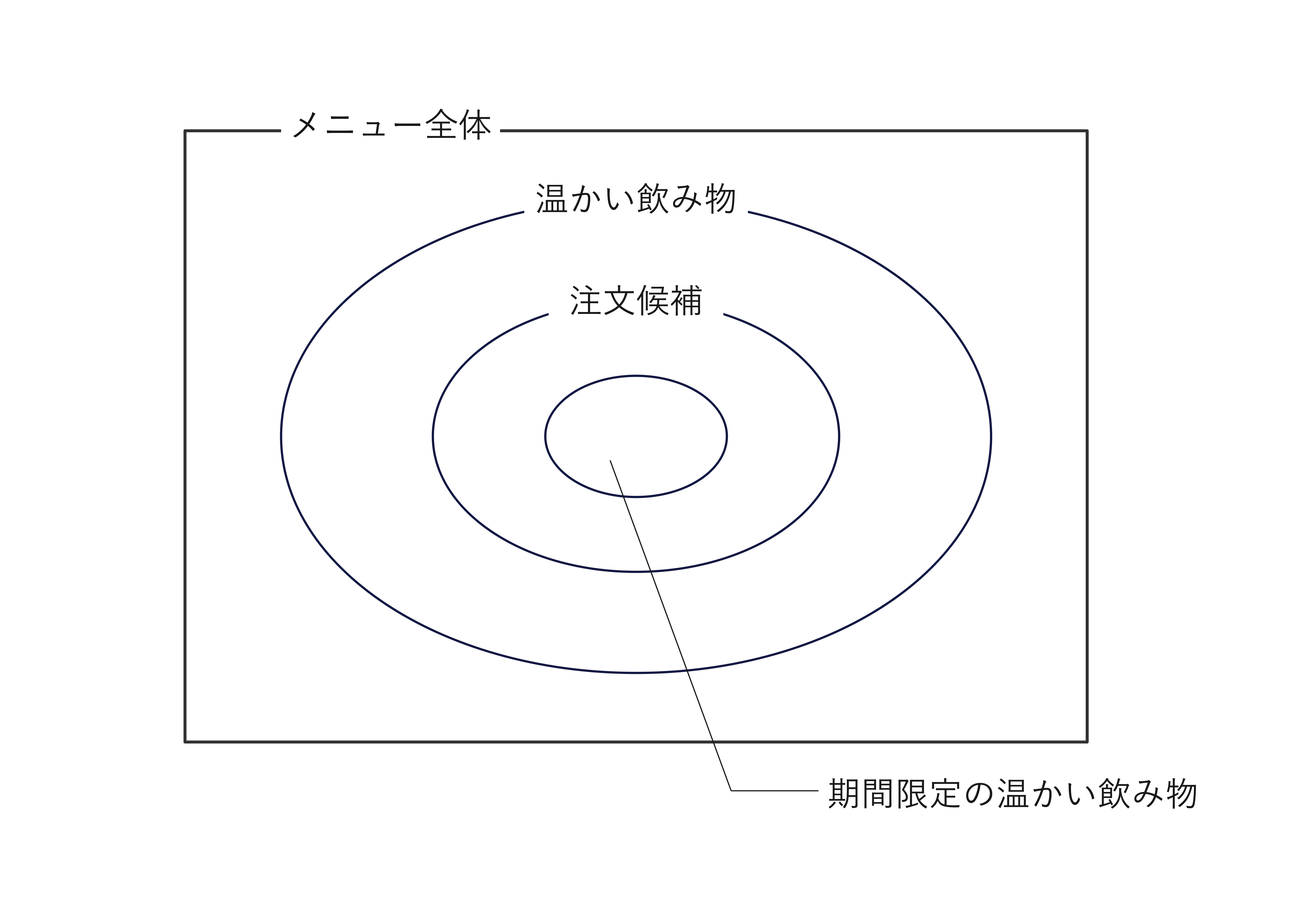
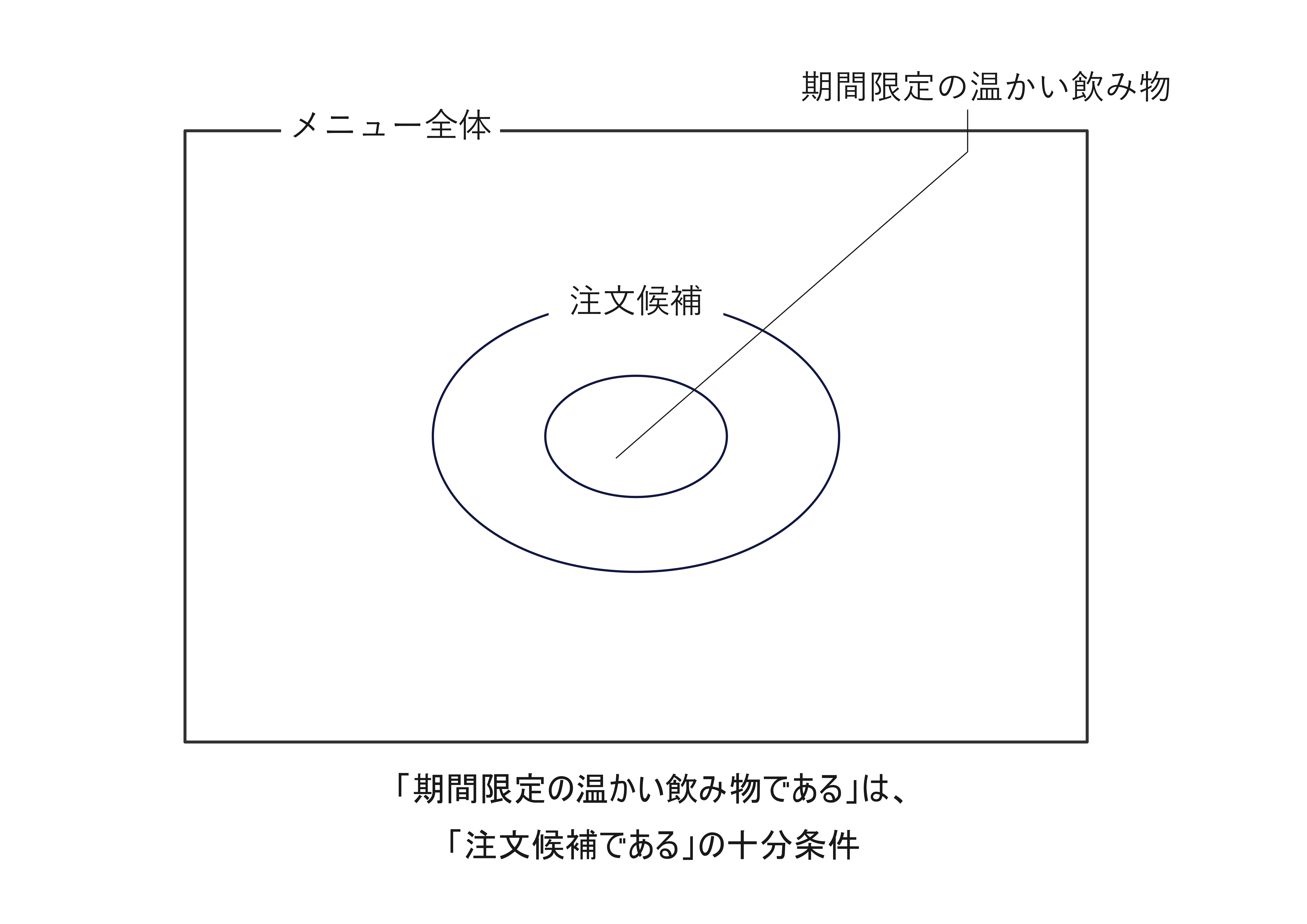
例えばお店に入って飲み物を注文する場面を考えます。あなたは注文する飲み物の候補を考えています。 まずその日は寒かったので、温かい飲み物から選ぶ必要があると考えました。そして候補になる条件はいろいろありますが、 特に期間限定メニューが気になっていたので、期間限定メニューの温かい飲み物であれば候補として十分だと考えました。
ここまでの流れを整理してベン図にすると下の図のようになります。
イメージとしては、温かい飲み物であることは注文候補であることの「より大まかな・緩い・粗い」条件で、 反対に期間限定の温かい飲み物であることは注文候補であることの「より具体的な・厳しい・細かい」条件といったところでしょうか。
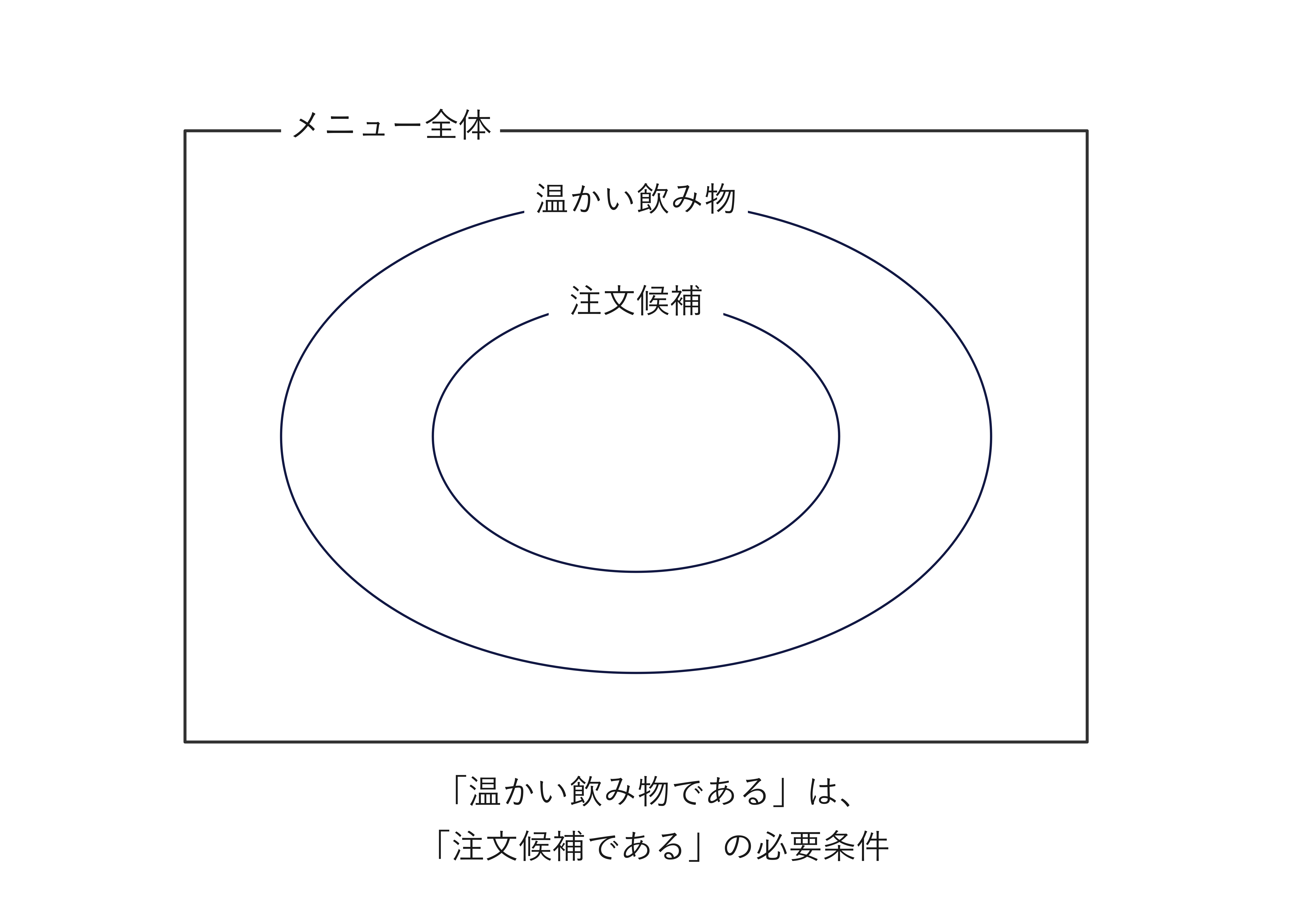
この「より大まかな・緩い・粗い」・「より具体的な・厳しい・細かい」がそれぞれ「必要」・「十分」に対応します。 つまり、\(x\)を飲み物として条件\(R(x)\)を「\(x\)は注文候補である」、 条件\(S(x)\)を「\(x\)は温かい飲み物である」、条件\(T(x)\)を「\(x\)は期間限定メニューの温かい飲み物である」とすると、 \(S(x)\)は\(R(x)\)であるための必要条件であるといえて、\(T(x)\)は\(R(x)\)であるための十分条件であるといえます。
必要十分条件と集合の相等
目次\(x\)についての2つの条件\(P(x),\) \(Q(x)\)について、2つの命題「\(P(x) \Rightarrow Q(x)\)」と「\(Q(x) \Rightarrow P(x)\)」を 「かつ」で結んだ命題「\(P(x) \Rightarrow Q(x)\)かつ\(Q(x) \Rightarrow P(x)\)」を\(P(x) \Leftrightarrow Q(x)\)と書きます。 \(P(x) \Leftrightarrow Q(x)\)が真であるとき、条件\(P(x)\)は条件\(Q(x)\)であるための必要条件でもあり、十分条件でもあります。 このとき条件\(P(x)\)は条件\(Q(x)\)であるための必要十分条件であるといいます。 もちろん、条件\(Q(x)\)は条件\(P(x)\)であるための必要十分条件であるともいえます。
さらに、このとき条件\(P(x)\)と条件\(Q(x)\)は同値(な条件)であるといいます。そして同値な条件に書き換えることを同値変形といいます。 今回の例を使うと、\(P(x) \Leftrightarrow Q(x)\)が真のとき、条件\(P(x)\)を条件\(Q(x)\)に書き換えたり、 条件\(Q(x)\)を条件\(P(x)\)に書き換えたりすることを同値変形と呼びます。
先程と同様に集合との関係も見てみましょう。条件\(P(x),\) \(Q(x)\)の真理集合をそれぞれ\(A,\) \(B\)とします。 \(P(x) \Leftrightarrow Q(x)\)が真のとき、「すべての\(x\)について『\(x \in A\)ならば\(x \in B\)』かつ『\(x \in B\)ならば\(x \in A\)』」が真といえます。 このとき2つの集合\(A,\) \(B\)に属する要素が完全に一致します。そしてこのとき集合\(A\)と集合\(B\)は等しいといい、 \(A=B\)(\(B=A\)でも同じ)で表します。この状況をベン図で表すと下のようになります。
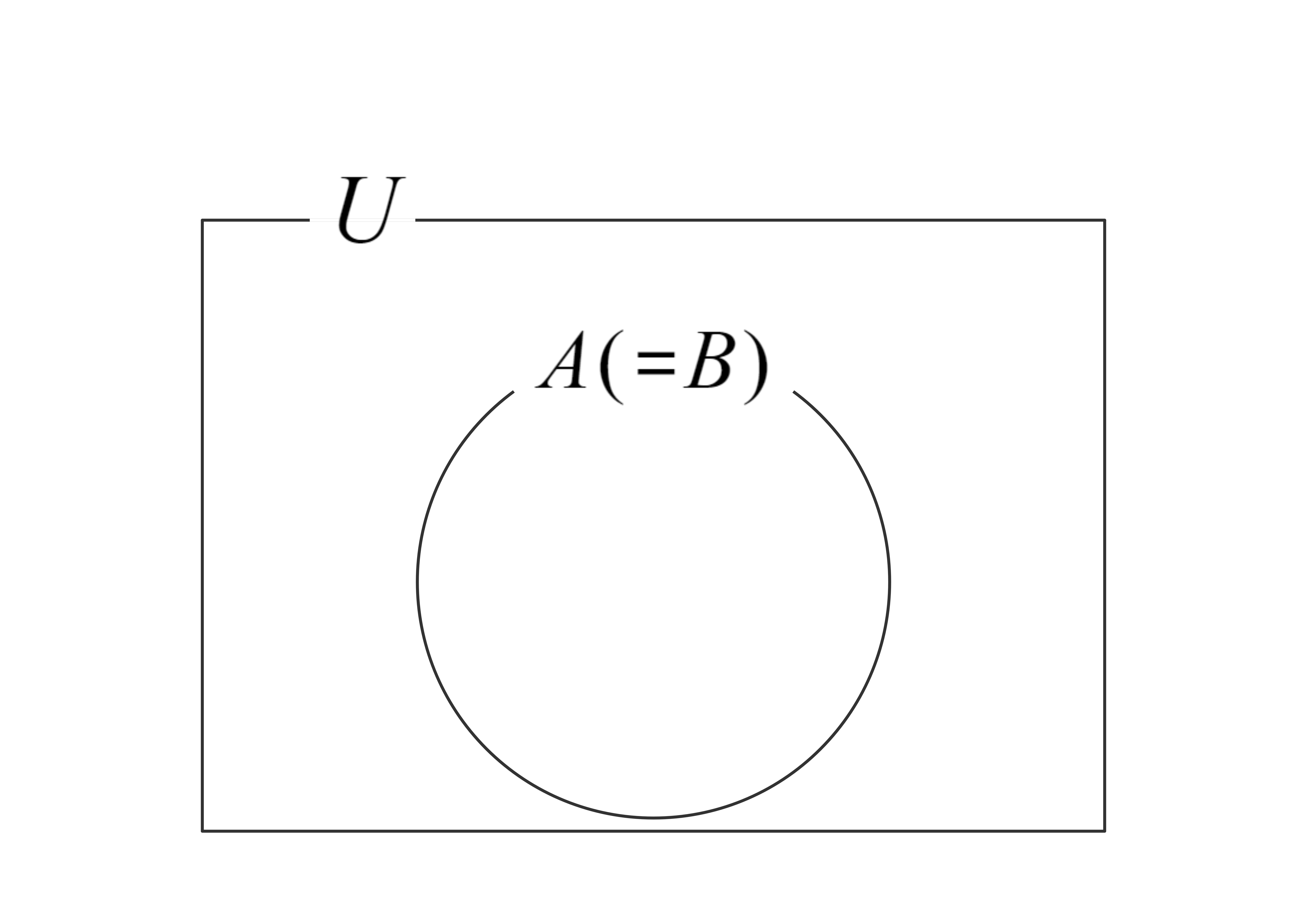
導出から分かるように\(A=B\)が成り立つことと、「\(A \subset B\)かつ\(A \supset B\)」が成り立つことは同じです。(\(A=B\)を「\(A \subset B\)かつ\(A \supset B\)」で定義することもあります。)
命題「\(P\)ならば\(Q\)」の注意点1
目次ここまでは厳密に「すべての\(x\)について『\(P(x)\)ならば\(Q(x)\)』」と書いてきましたが、 単に「\(P(x)\)ならば\(Q(x)\)」といった場合も頭に「すべての\(x\)について」を補って考えます。 実は、こちらの言い方のほうがよく使われます。数学ではこのように誤解の恐れがなければ「すべての」を省略することがしばしばあるので注意しましょう。
A. 厳密にはその通りです。とても鋭い質問なのでここまで気になった人はよく勉強していると思います。 高校数学で考える場面はほとんどありませんが、条件「\(P(x)\)ならば\(Q(x)\)」を前回学習した「かつ」・「または」・否定を使って表すと 条件「『\(P(x)\)でない』または『\(Q(x)\)』」と同値です。
この条件の真理集合をベン図で表すと下の図のようになります。
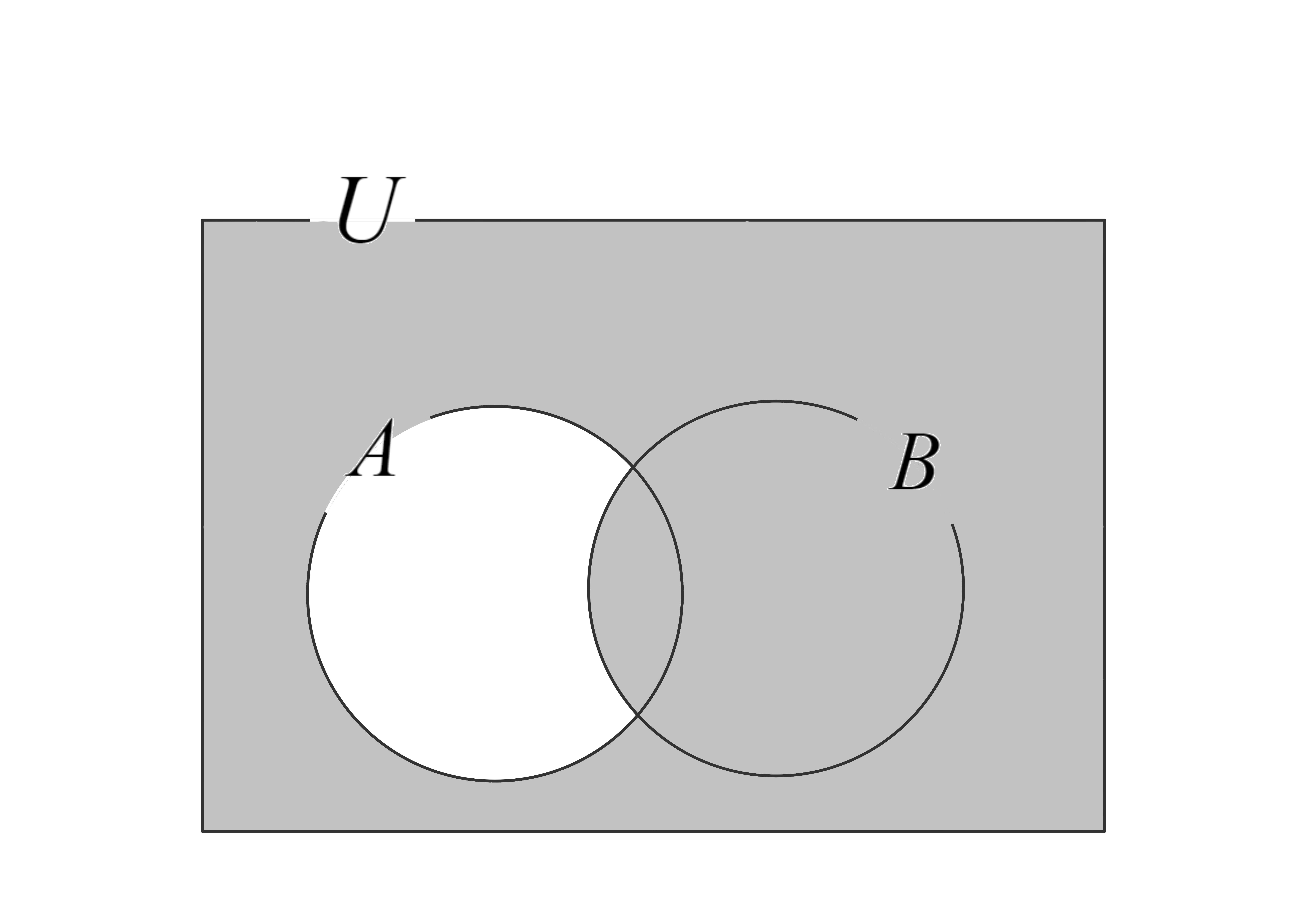
そして、この条件が「すべての\(x\)」について成り立つ場合、 たしかに\(A \subset B\)となります。
命題「\(P\)ならば\(Q\)」の注意点2
目次今までと同様に条件\(P(x),\) \(Q(x)\)の真理集合をそれぞれ\(A,\) \(B\)として、命題「\(P(x) \Rightarrow Q(x)\)」を考えます。 \(x\)が条件\(P(x)\)を満たさないときは条件\(Q(x)\)を満たしているか考える必要はないので、 もし条件\(P(x)\)を満たす\(x\)が存在しないとき、つまり\(A=\emptyset\)であるとき、このとき命題は条件\(Q(x)\)にかかわらず真になります。
(例)「\(x\)を実数として\(x^2\)が負ならば\(x\)は無理数である」は真
(補足)このとき、命題「\(P(x) \Rightarrow Q(x)\)」は「空ゆえに真」であるといいます。
また、集合との関係を確認すると\(\emptyset \subset B\)となります。 ここで、条件\(Q(x)\)はどんな条件でも良いので、それに対応して\(B\)も任意の集合をとることができます。 つまり、空集合はどんな集合に対しても、その部分集合となります。
2. 命題の証明方法
目次ここまでに様々な形式の命題を見てきました。ここではその証明方法を解説します。 ところで、「すべての」が付いた命題を全称命題、「ある」がついた命題を存在命題といいます。 この用語を覚える必要はないですが、説明を簡潔にするために解説で使用します。
直接証明法と間接証明法
目次命題を証明するのに、順に正しい推論を進め、証明する素直な方法を直接証明法といいます。これに対して、間接的に結論を導く方法を間接証明法といいます。 具体的には今から説明する背理法と後編の記事「必要条件・十分条件と命題の証明方法 (後編)」で登場する対偶証明法があります。
背理法とは命題が真であることを証明するのに、その命題が成り立たない(=偽である)と仮定して矛盾を導くことで命題が成り立つ(つまり、真である)ことを証明する方法です。 最初は分かりづらい考え方なので、一旦例題を見てみましょう。
(補足)間接証明法には他にも転換法・同一法などがあります。ほとんど使われませんが、数学Ⅰの 「2次方程式・不等式を解く(準備中)」で転換法を使う例が登場するので気になる人はご覧ください。
この例題を解いて背理法がどんなものか見てみましょう。はじめに、偽であると仮定するということはもとの命題を否定しましょう。 つまり、「\(\sqrt{2}\)が有理数である」と仮定します。
ここから矛盾を示す方法はそれぞれの問題によって慣れが必要です。 今回の問題は頻出問題でしかも「有理数」の扱い方が学べるので解答の流れを頭に入れておきましょう。
まず、有理数であることをどのように数式で表すかが問題です。定義に戻って考えると有理数とは分数の形に表される数なので、\(\dfrac{p}{q}\)と表しましょう。 ただし、ここで約分可能だと扱いにくいので約分がこれ以上できない形とします。このような分数を既約分数といいます。
約分がこれ以上できない形としたのに議論を進めていくと約分ができてしまうことになるという矛盾を示します。解答は次のようになります。
(スマホでは横持ち推奨)
-
\(\sqrt{2}\)が有理数であると仮定すると、\(\sqrt{2}\)は自然数\(p,q\)を用いて次のように表される。 \[\sqrt{2}=\frac{p}{q} \qquad \left(\frac{p}{q}\text{は既約分数}\right)\]
このとき, \(p=\sqrt{2}q\)から\(p^2=2q^2\)⋯⋯①
よって, \(p^2\)は偶数であり, \(p\)も偶数である。⋯⋯(注)
したがって, \(p=2k\)(\(k\)は自然数)⋯⋯② と表される。②を①に代入すると \[4k^2=2q^2 \quad \text{すなわち} \quad q^2=2k^2\] よって, \(q^2\)は偶数であり, \(q\)も偶数である。
つまり, \(p\)も\(q\)も偶数となるが, これは\(\dfrac{p}{q}\)が既約分数であることに矛盾する。
したがって, \(\sqrt{2}\)は無理数である。(注)厳密には「\(p^2\)が偶数であるならば, \(p\)も偶数である」を証明する必要があります。この命題の証明には次回学習する対偶証明法を使います。
背理法はもとの命題を否定したものを仮定することと、 有理数は\(\dfrac{p}{q}\)\(\left(\dfrac{p}{q} \text{は既約分数}\right)\)で表すことを覚えておきましょう。
ところで、この背理法はどこで使えるのかを見極めるのが難しいです。 なので、この前編後編が終わった次の記事「背理法の使い時まとめと複数の文字を含む条件」でまとめたので気になる人はご覧ください。
また、この問題にはいくつか別解があるので興味のある人は見てみてください。 さらなる別解は「無理数まとめ3選(準備中)」に掲載しています。
\(\sqrt{2}\)が有理数であると仮定すると, 整数\(p,\) \(q\)を用いて\(\sqrt{2}=\dfrac{p}{q}\)と表せます。(既約分数でなくてもいい)
このとき, \(p^2=2q^2\)となりますが, ここで両辺の素因数2の個数を比較したいと思います。 同じ数の素因数を考えているので素因数の個数は一致するはずです。詳しくは「素因数分解の一意性(準備中)」をご覧ください。
しかし, 2乗に注目すると\(p,\) \(q\)の偶奇にかかわらず左辺は2が偶数個, 右辺は2が奇数個となり矛盾します。
したがって, \(\sqrt{2}\)は無理数です。
この解法は素因数分解の一意性を利用して矛盾を示しています。
\(\sqrt{2}\)が有理数であると仮定すると, 自然数\(p,\) \(q\)を用いて\(\sqrt{2}=\dfrac{p}{q}\)⋯⋯①と表せます。(既約分数でなくてもいい)
このとき, 解答に示したように\(p\)も\(q\)も偶数になります。
つまり、自然数\(p,\) \(q\)が①を満たせば、自然数\(\dfrac{p}{2},\) \(\dfrac{q}{2}\)も①を満たします。 このことを繰り返すといくらでも小さい自然数が存在することになります。(永遠に2で割れるから)
しかし, 自然数には最小値1が存在するのでこれは矛盾です。
したがって, \(\sqrt{2}\)は無理数です。
この解答は無限降下法と呼ばれる手法を用いて矛盾を示しています。 無限降下法について詳しく知りたい方は「無限降下法(準備中)」をご覧ください。
全称命題の証明方法
目次ここからは命題の中でも「すべての」が付いた全称命題と「ある」が付いた存在命題の真偽の証明方法を詳しく見ていきます。
まず、全称命題「すべての\(x\)について\(P(x)\)」は\(x\)が何であってもいつも条件\(P(x)\)が成り立つことを示すので、 \(P(x)\)を式変形したりして真であることを示します。難しく聞こえますが、雑に言ってしまえば直感通りです。 ただ、この作業をもう少し丁寧に説明すると次のようになります。
先程の説明をよく見ると\(P(x)\)は条件なので真偽を判断するというのは厳密にはおかしいです。 なぜこのような説明をしたのか解説していきます。
全称命題の証明は厳密には次のように考えます。
- 全体集合\(U\)の不特定の要素\(a\)を変数\(x\)に代入して、命題\(P(a)\)を考えます。
- 命題\(P(a)\)が真であることを証明します。
こうすれば、全体集合\(U\)のどんな要素を代入しても命題\(P(a)\)が真であることがわかるので、全称命題を示せたことになります。 ところで、\(x\)に\(a\)を代入する操作は結果を見ると文字を変えただけになっています。 そこで、\(P(x)\)の時点で\(x\)は全体集合\(U\)の不特定の要素であると考えて、命題\(P(x)\)が真であることを証明すれば良さそうです。
このような背景から「\(P(x)\)が真であることを示す」と解説しました。
普段はあまりしませんが、偽であることを証明するときもあります。これは簡単で、「すべての」が間違っていることが示すには例外が存在することを示せばいいです。 この例外を反例といいます。
また、先程学んだ背理法を用いて真であることを証明する場合は偽であることを仮定して矛盾を導くので、 反例が存在すると仮定して矛盾が生じることを示します。
全称命題の真偽を答えるときは、まず反例がないか簡単な数で調べましょう。 見つからないときは真であると予想して証明を考える作業に移りましょう。
\(x=0\)が反例です。よって、偽となります。
\(x^2+2x+2\)の値は
\begin{align} &x=0 \text{のとき, } 2\\[0.7em] &x=1 \text{のとき, } 5\\[0.7em] &x=-1 \text{のとき, } 1 \end{align}
となり、反例が見つからなさそうなので証明を考えます。
ポイントは2つある\(x\)を1つにまとめることです。 というのも、この式のまま考えると\(x\)の値によって\(x^2\)も\(2x\)も動いてしまうので、全体の動きが掴めません。 2次関数を学習すると出てくる考え方ですが先取りして覚えておきましょう。 どのようにまとめるかというと\(x^2+2x+1= {} \)\((x+1)^2\)を使います。すると、
\[x^2+2x+2=(x+1)^2+1\]
となります。\((\text{実数})^2 \geqq 0\)なので、\((\text{右辺}) > 0\)となり、正であることが示せたので証明完了です。 「2つある\(x\)を1つにまとめる」操作について詳しく知りたい人は2次関数分野の記事「さまざまなグラフ・グラフと方程式のつながり(準備中)」をご覧ください。
- 偽である。反例は\(x=0\)
-
真である。
(証明)\[x^2+2x+2=(x+1)^2+1>0\] よって, すべての実数\(x\)について, \(x^2+2x+2\)は正である。
存在命題の証明方法
目次存在命題と聞くと仰々しく聞こえますが、要は存在することを示せばいいだけです。つまり、次のようにして証明します。
- 条件を満たすものを例示する
- 例示したものが条件を満たすことを証明する
条件を満たすものを見つけてきてたしかに成り立つことを示せば終わりです。 このときどうやって条件を満たすものを見つけたのかは書く必要がありません。 なので、唐突に書き出して大丈夫です。
また、きちんと具体的に例示することも大切です。
きちんと例示しなかったために結論がおかしくなってしまった例を紹介します。
Q. 命題「ある自然数\(x\)について\(x^2+2x+1=0\)」の真偽を答えて、さらに証明してください。
(誤答例)
\(x^2+2x+1=(x+1)^2\)なので\(x+1=0\)のとき\(x^2+2x+1=0\)
よって, 真である。
一見それっぽいですが、よく考えると\(x+1=0\)となるような自然数\(x\)がそもそも存在しないので間違っています。 このようなミスをしないために具体的に例示しましょう。
そして偽であることを証明する場合は、条件を満たすものが存在してはいけないので「すべての要素が条件を満たさない」を証明します。 実はこれは全称命題になっています。この現象は「すべての」と「ある」の否定がそれぞれ「ある」・「すべての」と入れ変わることに関係しています。 見直してみると先程の全称命題が偽であることの証明の「反例が存在する」も存在命題です。
また、背理法では「すべての要素が条件を満たさない」と仮定して矛盾を示します。 注意点としてこの方法で証明された場合、条件を満たすものが存在することは分かっても具体的な値は分からないままとなります。
存在命題の真偽を答えるときは、まず条件を満たす例が存在するか簡単な数で調べましょう。見つからないときは偽であると予想して証明を考える作業に移りましょう。
\(x=0\)のとき\(x^2+2x-1=-1 < 0\)です。したがって命題は真です。
(1)で気づいた人もいるかもしれませんが例題3は例題2の否定になっています。 なので、(2)は偽なのですが、その証明は 「すべての実数\(x\)について、\(x^2+2x+2\)は正である。(=だから\(x^2+2x+2\)が0以下になるような実数\(x\)は存在しない。)」ことを示せばよいです。 つまり、例題2の(2)と同じ流れです。
\(x^2+2x+2=(x+1)^2+1>0\)より、命題は偽です。
- \(x=0\)のとき\(x^2+2x-1=-1 < 0\)より, 真である。
-
偽である。
(証明)\[x^2+2x+2=(x+1)^2+1>0\] よって, \(x^2+2x+2\)が\(0\)以下になるような実数\(x\)は存在しない。
ここまで見てきたように全称命題と存在命題はコインの表と裏のような関係になっています。 それぞれの証明方法について表にまとめると下のようになります。
| 全称命題 | 存在命題 | |
|---|---|---|
| 真 | 全部示す | 見つける |
| 偽 | 見つける | 全部示す |
※背理法で真であることを示すときは偽のときの方法で進めて矛盾を示す。
3. まとめと次回予告
目次まとめ
目次今回の内容をまとめると、
- \(Q \Rightarrow P\)が真のとき\(P\)は\(Q\)であるための必要条件、\(P \Rightarrow Q\)が真のとき\(P\)は\(Q\)であるための十分条件、\(P \Leftrightarrow Q\)が真のとき\(P\)は\(Q\)であるための必要十分条件
- 空集合はどんな集合に対しても、その部分集合
- もとの命題を否定したものを仮定して矛盾を示すのが背理法
- 全称命題・存在命題を証明するときは「全部示す」のか「見つける」のか考える
次回予告
目次後編ではいよいよ頻出の「\(P\)ならば\(Q\)」型命題の証明方法を扱います。 この形の命題は「すべての」が省略されていたので全称命題の考え方を使えば証明することができそうです。 また、今回登場した背理法以外の間接証明法である対偶証明法についても学びます。
そして、「\(P\)ならば\(Q\)」型命題をきちんと証明することができるようになったところで今回学んだ必要条件・十分条件を実際に判別する問題を解いていきます。