連立方程式・不等式と「変数」・「定数」
最終更新日:
この記事では連立方程式の復習として加減法や代入法を振り返るとともに、前回学習した不等式が連立された連立不等式の解き方を解説します。また、方程式や関数の分野で登場する「変数」や「定数」という言葉のイメージとそれを使った問題のレベル分けを紹介します。
目次
1. この記事を読むのに必要な前提知識
目次この記事で出てくる用語の解説とそれを詳しく扱っている記事へのリンク集です。
「2の倍数である」と「偶数である」のように2つの条件が数学的に同じ意味を持つとき「2つの条件は同値である」という。 また、もとの条件と同値な条件に変形することを同値変形という。 方程式や不等式を解くことは与えられた条件と同値な最も簡単な形(\(x= {}\)〇〇など)の条件を答えることだと捉えることができる。
両辺を乗除するときに注意が必要で、等式の場合と異なり、\(a >0\)のときは不等号の向きが変わらないが、 \(a > 0\)のときは不等号の向きが変わる。1次不等式の詳しい解説は前回の記事参照。
数\(a\)に対して、原点からの距離を\(a\)の絶対値といい、記号\(|a|\)で表す。 この定義より実数の範囲では、\(A \geqq 0\)のとき\(|A|=A,\) \(A < 0\)のとき\(|A|=-A\)となる。 詳しい解説は前回の記事参照。
2. 連立方程式の加減法・代入法と同値
目次連立方程式は中学数学でも登場し、「加減法」と「代入法」といった解き方を学んだと思います。 どちらも方程式に含まれる文字の数を減らすことが狙いです。 この考え方は、より一般の連立方程式を解くときも基本になります。
この記事では「加減法」と「代入法」を同値変形を意識して復習します。 中学数学では基本的に解が1つなので、この同値変形を意識しなくてもほとんど問題が起きませんでしたが、高校数学では答えが1つとは限らないので問題が起きることがあります。 連立方程式を正確に解くためにここで確認しておきます。
連立方程式\(\begin{cases}\text{①}\\[0.5em] \text{②}\end{cases}\)を考えます。(丸数字は式を表します。)
-
加減法
①と②から加減法によってできた式を③とすると、
\[\begin{cases}\text{①}\\[0.5em] \text{②}\end{cases} \iff \begin{cases}\text{①}\\[0.5em] \text{③}\end{cases} \iff \begin{cases}\text{②}\\[0.5em] \text{③}\end{cases}\]
が成り立ちます。
-
代入法
②を①に代入した式を③とすると、
\[\begin{cases}\text{①}\\[0.5em] \text{②}\end{cases} \iff \begin{cases}\text{③}\\[0.5em] \text{②}\end{cases}\]
が成り立ちます。
日本語に直して考えてみます。まず加減法の場合、加減法によってできた式と元の式のどちらかを残す必要があります。 どちらを残しても同値が保たれるので、実は同値変形を意識していなくても問題が起きにくいです。
それに対して問題が起きやすいのが次の代入法です。代入法は必ず代入してできた式と代入元の式を残す。 代入法では残す式を間違えると同値関係が崩れます。例を見て確認してみましょう。
中学数学で連立方程式を学んだときに「連立方程式の解はグラフの交点の座標を表す」ことを習ったと思います。 これを利用して、まずは答えがいくつあるか調べてみます。
第9回「必要条件と十分条件・命題の証明方法 (後編)」の例題4の(3)に出てきたように、\(x^2+y^2\)は原点からの距離の2乗を表します。 つまり、\(x^2+y^2=r^2\)は原点を中心とした半径\(r\)の円を表します。 よって、\(x^2+y^2=2\)と\(y=x\)のグラフを描くと次のようになります。
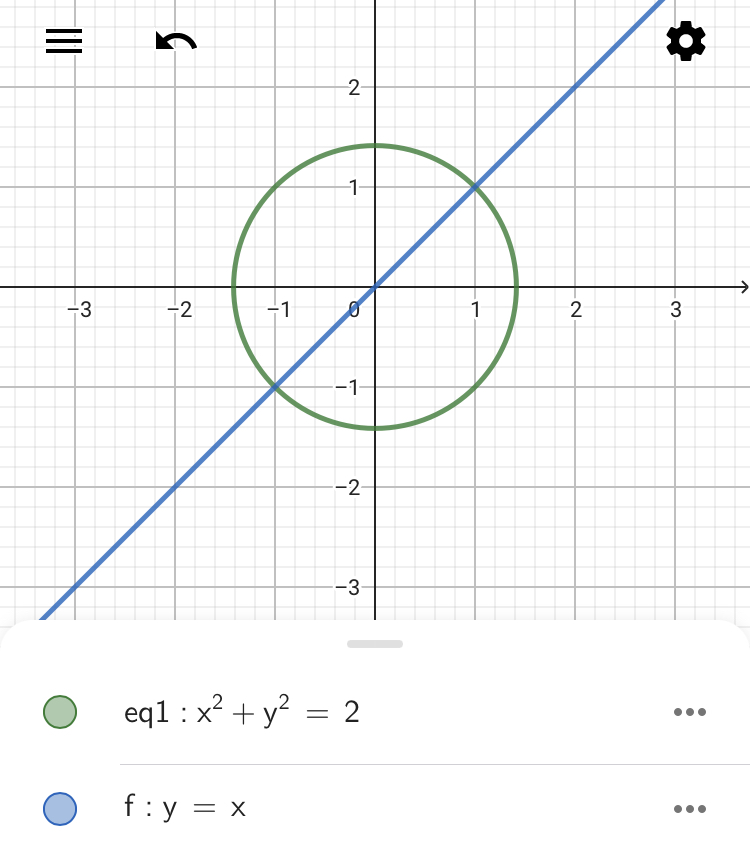
グラフを見ると分かるように交点は2つです。したがって、連立方程式の解も2つになるはずです。それでは代入法によって、解いていきます。
\(\begin{cases}x^2+y^2=2 & \cdots\cdots\text{①}\\[0.5em] y=x & \cdots\cdots\text{②}\end{cases}\)とします。
②を①に代入した式を③とすると
\[x^2+x^2=2\cdots\cdots\text{③}\]
今回の本題はここからです。③と②を残した場合(正しい場合)と③と①を残した場合(間違っている場合)を比べます。
[1] ③と②を残した場合(正しい場合)
③より
\begin{align} 2x^2 &= 2\\[0.7em]x^2 &= 1\\[0.7em]x &= \pm1\\[0.7em] \end{align}
これを②に代入して解を求めると
\[(x,y)=(1,1),(-1,-1)\]
[2] ③と①を残した場合(間違っている場合)
③より
\begin{align} 2x^2 &= 2\\[0.7em]x^2 &= 1\\[0.7em]x &= \pm1\\[0.7em] \end{align}
これを①に代入して
\begin{align} (\pm1)^2 + y^2 &= 2\\[0.7em]y^2 &= 1\\[0.7em]y &= \pm1\\[0.7em] \end{align}
したがって、解は
\[(x,y)=(1,1),(1,-1),(-1,1),(-1,-1)\]
このように、代入法の同値変形を誤ると答えが異なる場合があります。実はこの異なり方を調べると必ず余分な答えが出てくる形になっています。 これは間違っている場合が\(\begin{cases}\text{①}\\[0.5em] \text{②}\end{cases} \implies \begin{cases}\text{①}\\[0.5em] \text{③}\end{cases}\)でしかないこと、つまり元の連立方程式の必要条件であるが, 十分条件ではないことが原因です。
連立する方程式の数が多くなったり、複雑になったりすると見落としがちになるので注意しましょう。
- \((x,y)=(1,1),(-1,-1)\)
3. 連立不等式の解法
目次連立不等式では「加減法」や「代入法」が使えないので、「それぞれの不等式が表す範囲を考えて、それらを合体させる」ことが基本的な解法になります。 このときに要になるのが必要条件と十分条件・命題の証明方法 (後編)でも登場した次の考え方です。
1変数は数直線、2変数は座標平面の利用を考える
よりわかりやすく不等式の場合で言い換えると 「\(x\)についての不等式は数直線、\(x,y\)についての不等式は座標平面で考える」ということになります。 このように不等式は、図示して視覚的に解くことが効果的なので、次の例題で試してみましょう。
次の不等式を解いてください。(4)は不等式が表す範囲を図示してください。
- \(\begin{cases}6x+3 \geqq 2x-5\\[0.5em] 2x+11 > 8x-7\end{cases}\)
- \(|2x+5| < x+3\)
- \(\begin{cases}|2x+7| > -x\\[0.5em] |x+5| \leqq 15\end{cases}\)
- \(\begin{cases}x^2+y^2 \leqq 9\\[0.5em] x \leqq 0\end{cases}\)
※各解説・解答からこの例題に戻れます
まずは、それぞれの不等式を解いていきます。一つ一つの不等式は前回学習した1次不等式です。
\(6x+3 \geqq 2x-5\)を解くと
\begin{align} 4x &\geqq -8\\[0.7em]x &\geqq -2\\[0.7em] \end{align}
\(2x+11 > 8x-7\)を解くと
\begin{align} -6x &> -18\\[0.7em]x &< 3\\[0.7em] \end{align}
各不等式が解けたらいよいよ数直線の出番です。連立不等式なので2つの不等式が表す範囲の共通部分を求めましょう。
(数直線載せる)
よって、答えは\(-2 \leqq x < 3\)となります。
絶対値が出てきたので前回の復習をします。絶対値は原則、中身の正負で場合分けしますが、いくつか特殊な外し方があることを紹介しました。それがこちらです。
- \(|A|=B \iff B \geqq 0 \text{かつ} A= \pm B\)
- \(|A|=|B| \iff A= \pm B\)
- \(|A| < B \iff -B < A < B\)
- \(|A| >B \iff A < -B \text{または}B < A\)
補足:3,4は等号が付いてもいいです。また、\(B \geqq 0\)という条件は必要ありません。
(2)は3の形になっているので、これを使いましょう。
\begin{align} &|2x+5| < x+3\\[0.7em]\iff&-(x+3) < 2x+5 < x+3\\[0.7em]\iff&\begin{cases}-(x+3) < 2x+5\\[0.5em] 2x+5 < x+3\end{cases}\\[0.7em] \end{align}
ここまで来ればあとは(1)と同様です。
\(-(x+3) < 2x+5\)を解くと
\begin{align} -3x &< 8\\[0.7em]x &> -\dfrac{8}{3}\\[0.7em] \end{align}
\(2x+5 < x+3\)を解くと
\begin{align} x &< -2\\[0.7em] \end{align}
2つの不等式が表す範囲の共通部分を求めると
(数直線載せる)
よって、答えは\(-\dfrac{8}{3} < x < -2\)となります。
絶対値を含む不等式が連立されてもやることは同じです。まずはそれぞれの不等式を解いていきます。\(|2x+7| > -x\)を解くと
\begin{align} &2x+7 < x \text{または} -x < 2x+7\\[0.7em]\iff&x < -7 \text{または} -\dfrac{7}{3} < x\\[0.7em] \end{align}
\(|x+5| \leqq 15\)を解くと
\begin{align} &-15 \leqq x+5 \leqq 15\\[0.7em]\iff&-20 \leqq x \leqq 10\\[0.7em] \end{align}
「または」と「かつ」に注意して答えを求めます。 一度に考えるのが大変な人は「(\(A\)または\(B\))かつ\(C\)\(\iff\)(\(A\)かつ\(C\))または(\(B\)かつ\(C\))」を使ってもいいです。(普段の分配法則と同じ要領です。「かつ」と「または」を入れ替えても成り立ちます。) この法則の証明が気になる人は「数理論理学(準備中)」をご覧ください。
(数直線載せる)
したがって、答えは\(-20 \leqq x < -7\)または\(-\dfrac{7}{3} < x \leqq 10\)となります。
数1の数と式分野では登場しませんが、2文字の場合を出題しました。2文字のときは座標平面で考えます。 このとき答え方は図示して答えるのが一般的です。数2でよく登場するので今のうちに慣れておきましょう。
それぞれの不等式の図示について、まず\(x^2+y^2 \leqq 9\)は例題1 代入法の同値変形の\(x^2+y^2=r^2\)の例から類推できそうです。
\(x \leqq0\)の方は\(y\)が含まれていないので困惑するかもしれませんが、含まれていないということは「何でもいい」という意味になります。 以上から連立不等式が表す範囲を図示してみましょう。
(座標平面載せる)
\(\leqq\)の表現については図にあるように「境界を含む」と書いて示します。
- \(-2 \leqq x < 3\)
- \(-\dfrac{8}{3} < x < -2\)
- \(-20 \leqq x < -7\)または\(-\dfrac{7}{3} < x \leqq 10\)
- (座標平面載せる)
4. 「変数」と「定数」とは
目次ここからは方程式や関数で登場する「変数」と「定数」とは何かのイメージを紹介します。 さらに、「変数」と「定数」に注目して問題の複雑さをレベル分けしていきます。 これを知っておくと、次の単元の2次関数の問題が解きやすくなると思います。
「変数」と「定数」のイメージ
目次前回の記事「1次不等式と場合分け」の例題1 1次方程式・不等式で「定数」という言葉が出てきました。 また、「定数」の対になる言葉として、「変数」という言葉もあります。 方程式や関数を扱うときにこれらの用語を目にすることがあるので、ここでイメージを掴んでおきましょう。
- 変数…関数や方程式で、主役になる文字
- 定数…関数や方程式で、脇役になる文字
「主役」とは「〇〇は××の関数である」の〇〇や××に入る文字や「△△についての方程式」の△△に入る文字です。 そして、「脇役」はそれ以外の文字のことです。なぜ、ここに入る文字が主役かというと状況設定において重要な役割を果たすからです。
例えば「\(y=ax\)のグラフを描いてください。」と言われたら比例のグラフを思い浮かべると思います。 これは\(y\)を\(x\)の関数とみて、\(a\)は傾きを表す文字だと解釈したためです。 つまり、\(x\)と\(y\)を主役(=変数)とみて、\(a\)を脇役(=定数)とみています。 もしここで、主役と脇役を間違えるとどうなるでしょうか。
試しに、3つの文字すべてが主役(=変数)とみた場合は、「\(y\)を\(a\)と\(x\)の関数」とみることになります。 このとき、グラフは以下のようになります。
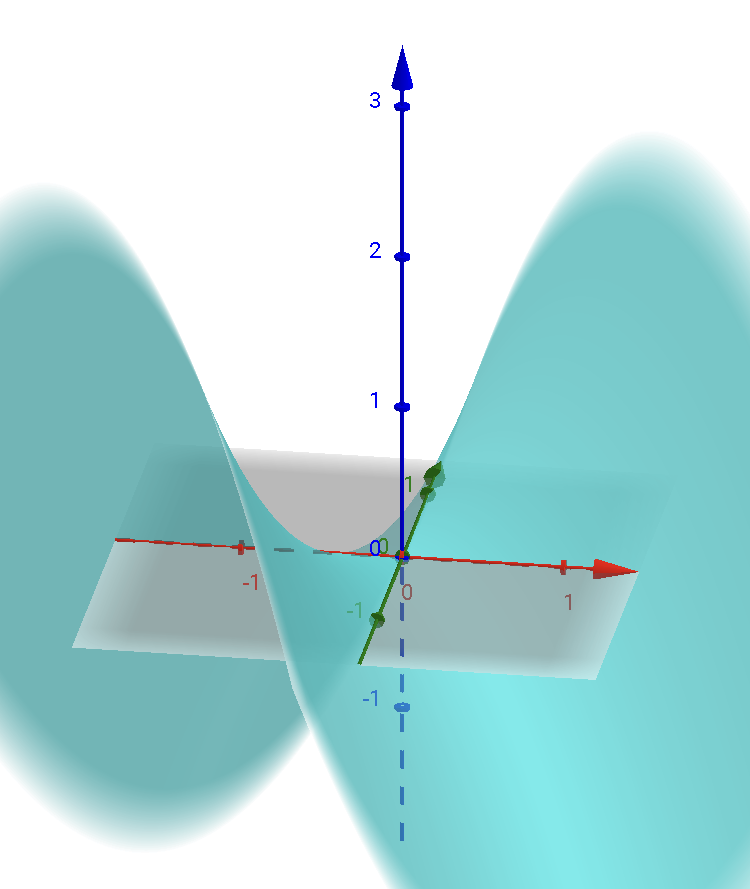
急に見慣れない形ですが、グラフは3次元になりました。このように、主役と脇役を間違えると状況設定が全く別物になってしまうので注意です。 ちなみになぜこのようなグラフになるかというと、まず\(y=ax\)(比例)のグラフを傾きをだんだん大きくしてパラパラ漫画のように手前から奥に並べます。 それらを合成するとこの形になるのが見えてくると思います。
注意が必要と言いましたが、\(y=ax\)の例を出したときほとんどの人は比例のグラフを思い浮かべたでしょうし、私も比例のグラフを想定して書きました。 慣例的に変数つまり主役は\(x,y,\cdots\cdots\)、定数つまり脇役は\(a,b,\cdots\cdots\)を使うからです。
このように数学では文字の使用に慣例があります。 なので、自分で文字おきして状況設定をする際に、どの文字を使うか迷うことがあります。 そんな人のために「数学で使う文字の慣例(準備中)」でどの文字が適任かまとめたので興味のある人はご覧ください。 (もちろん、慣例から外れていてもきちんと説明すれば問題ないですし、慣例通りだとしても自分で文字おきしたときは丁寧に説明しましょう。)
まとめとして繰り返すと、「変数」と「定数」のイメージは状況設定の主役と脇役です。
補足:方程式では主役の文字のことを「未だに値を知らない数」から「未知数」と呼ぶこともあります。
「変数」と「定数」から考える問題の複雑さ
目次「変数」と「定数」のイメージを掴んだところで、この2つに注目して問題の複雑さをレベル分けしたいと思います。 レベルが高いほど問題の論理構造が難しい、つまり、「何言ってるの、この問題??」となりやすいことを意味します。(注:計算の難しさではありません。)
- LEVEL1 変数しか登場せず、変数についての条件を求める問題
- LEVEL2 変数と定数が登場し、変数と定数についての条件を求める問題
- LEVEL3 変数と定数が登場し、変数が〇〇となるような、定数についての条件を求める問題
この文章が「何言ってるの?」となりそうなので、具体例で考えます。\(x\)についての2次方程式をテーマにして各レベルの問題がどのようなものか見ていきます。
小問番号がLEVELに対応しています。この問題では\(x\)が変数、\(a\)が定数ですね。それでは順番に具体例を見ていきます。
(1)はとても簡単です。変数\(x\)しか登場せず、定数\(a\)は登場していません。 3つのレベルの中で、一番基本的で簡単な形で、ここから発展してLEVEL2,3になります。 もちろん答えは\(x=±2\)です。
今度は定数\(a\)が加わりました。なので、方程式の解は定数\(a\)を使って表すことになります。 これが変数と定数についての条件を求めるLEVEL2の形です。
このパターンは定数の値によって答えが変わることが多く、その場合、正確に場合分けをして求めることができているかが採点ポイントになります。 計算が同じになるものをまとめて処理し、異なるものは区別して、しっかりと全パターンを網羅するように気を付けましょう。
2乗して\(a\)になるものが\(x\)なので\(a\)が0以上かどうかで解が変わります。 答えは \(\begin{cases} x=\pm\sqrt{a} & (a \geqq 0) \\[0.5em] \text{解は存在しない} & (a < 0) \end{cases}\) となります。
(2)を解いた後だとわかりやすいですが、中学数学までではあまり見ない新しいパターンの問題で、構造も複雑です。 この問題では解が存在する条件つまり、変数\(x\)の存在条件が聞かれています。
ここで存在条件と聞いて「背理法の使い時まとめと複数の文字を含む条件」を思い出してくれた人は記事を読んでいただきありがとうございます。 この記事でも解説したように、変数\(x\)が存在するかどうかは変数\(x\)以外の文字次第、つまり、定数\(a\)次第です。 なので、この問題は定数\(a\)についての条件を答えることになります。(\(x\)の存在条件は\(x\)についての条件ではありません。)
答えは(2)を見れば簡単で、解が存在するのは\(a \geqq 0\)のときです。 \(x\)の2次方程式の問題ですが、答えに\(x\)がいないことに注意してください。
"定"数という言葉から考えると\(a \geqq 0\)ということは非負の実数を動く変数のようにも見えます。 しかし、\(a \geqq 0\)だからといって元の方程式を\(x\)と\(a\)についての方程式と見るようになったわけではありません。 あくまで\(a\)は脇役であり、主役\(x\)が存在するための条件は脇役\(a\)が\(a \geqq 0\)のときという意味です。
これは用語が紛らわしいのですが、「変数」と「定数」のイメージを変わる数・定まる数とするとわかりづらいです。 主役・脇役でイメージするのがおすすめです。
- \(x=±2\)
- \(\begin{cases} x=\pm\sqrt{a} & (a \geqq 0) \\[0.5em] \text{解は存在しない} & (a < 0) \end{cases}\)
- \(a \geqq 0\)
LEVEL3の「変数が〇〇となるような、定数についての条件を求める」の意味は掴めたでしょうか。次回はこの形の問題を解いていきます。 また、LEVEL3の頻出問題として「2次方程式の解の配置問題」があります。今回の記事で学んだイメージがあれば取り組みやすいと思います。
解の配置問題が気になる人は「解の配置問題(準備中) 」で詳しく解説しているのでそちらをご覧ください。
5. まとめと次回予告
目次まとめ
目次今回の内容をまとめると、
- 加減法は、加減法によってできた式と元の式のどちらかを残す
- 代入法は、代入してできた式と代入元の式を残す
- 連立不等式は数直線・座標平面を利用する
- 関数や方程式において変数は主役、定数は脇役のイメージ
- 変数が〇〇になるような条件は?と聞かれたら定数についての条件を答える問題
次回予告
目次今回と前回で扱った1次不等式、絶対値を含む方程式、連立方程式・不等式などをテーマにしたLEVEL3の問題を扱います。 「数と式・集合と命題」分野の最後の記事なのでぜひ読破を目指して頑張ってください。